Not enough info...
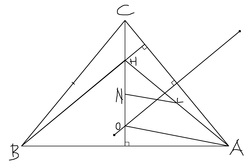 An acute isoceles triangle ABC has integer side lengths of a,b,c. The perpendicular feet are drawn from each angle and intersect at H. Then, each side is perpendicularly bisected to meet at O. Point N is drawn such that N is on segment
. Point L is drawn at the midpoint of line
such that
. Triangle
has an area of 48. If the sum of the two smallest possible lengths of
can be expressed as
for positive co-prime
x,y, find x+y.
An acute isoceles triangle ABC has integer side lengths of a,b,c. The perpendicular feet are drawn from each angle and intersect at H. Then, each side is perpendicularly bisected to meet at O. Point N is drawn such that N is on segment
. Point L is drawn at the midpoint of line
such that
. Triangle
has an area of 48. If the sum of the two smallest possible lengths of
can be expressed as
for positive co-prime
x,y, find x+y.
Also, this is probably the worst problem that I've made cuz this is just stupid hard and uses practically unknown formulas.
HINT: try to see if you can do it without this information below
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
One side length is 10 of both triangles.
The answer is 71.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Google 9-point center and read the wolfram mathworld entry it helps to under stand this solution.
This is the lazy way to do this problem, there is a way that is much more mathematical that requires much less knowledge than this one, see if you can figure it out.
The 9-pointcenter is halfway between the ortho center and circum center. The distance between the orthocenter (H) and circumcenter (O) is O H 2 = 9 ( 4 △ a b c ) 2 − ( a 2 + b 2 + c 2 ) where a,b,c are the sides and △ is the area of the triangle (the first half of the equation in parentheses=the circum radius). The first few heron triangles that have an area of 48 are (10,10,12) and (10,10,16). Plugging them in and dividing the answers by two we get
1 1 / 8 + 1 3 / 2 = 6 3 / 8 .
6 3 + 8 = 7 1