Not enough information!
There is a vertical pole perpendicular to the horizontal plane. From point P on the plane, 2 projectiles are fired simultaneously at different velocities. The first projectile is fired at an angle of 3 0 ∘ and it hits the foot of the pole. The second projectile is fired at an angle of 6 0 ∘ and it hits the top of the pole.
It is further known that the projectiles hit the pole at the same time.
If the angle subtended by the pole from P is α , find tan α to 3 decimal places.
Details and Assumptions:
- Air resistance is negligible.
- A gravitational pull is present.
The answer is 1.155.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Your first solution is amazing! I've learnt something from you, thank you!
Log in to reply
Me too..I also learnt it new... Now I will always consider changing the frame of reference
Oh, well done! That was a brilliant solution, to use a falling camera!
The approach of falling camera is super innovative and it greatly simplifies the problem. Kudos!
Your first approach is very nice!
I liked both the solutions! They are so simply put! I would like to know if you solved it first time with same steps as posted here...Because they're really elegant with no mess at all. When I solve these my solution looks a mess. Solving this elegantly feels difficult. I think you revise your steps and remove the reducible steps before posting solution, is it?
Log in to reply
No, this was my first attempt. However, I have some experience solving this kinds of problems. That helps finding the "elegant" approach!
I can't figure out the idea of the falling camera
Log in to reply
There is a correlation between the fact that the ground is moving and the projectiles have constant velocity ?
Essentially, the projectiles are in free fall. Relative to the ground, they gain 9 . 8 1 m s − 1 in downward velocity per second.
However, if we compare the position of the projectiles to that of something else in free fall, this downward acceleration no longer plays a role. This is why everything appears to be weightless in a free-fall environment (e.g. falling elevator, orbiting space station).
Another way of looking at this: take two projectiles and consider the vertical motions: { y 1 = y 1 , 0 + v 1 , 0 t − 2 1 g t 2 ; y 2 = y 2 , 0 + v 2 , 0 t − 2 1 g t 2 . The position of projectile 2 relative to projectile 1 we find by subtraction: y r e l = y 2 − y 1 = ( y 2 , 0 − y 1 , 0 ) + ( v 2 , 0 − v 1 , 0 ) t . This relative motion is linear ! I chose y 1 , 0 = 0 and v 1 , 0 = 0 , so that from the perspective of projectile 1, the falling camera, y r e l = y 2 , 0 + v 2 , 0 t .
Log in to reply
Thank you very much: very clear, smart and patient.
I will prove the general case: when the angle of the first projectile is α 1 and the angle of the second projectile is α 2 .
Let the initial velocity of the first projectile be v 1 and the initial velocity of the second projectile be v 2 . Furthermore, let the gravity experienced by the projectiles be g , the distance between P and the foot of the pole be d , the height of the pole be h , and T be the time taken for the projectiles to reach the pole.
I will break this question down into 5 parts.
Part 1:
Here, we will try to establish an initial relationship between α 1 and α 2 .
Firstly, note that there is no horizontal acceleration. The horizontal velocity for the first projectile is v 1 cos α 1 and the horizontal velocity of the second projectile is v 2 cos α 2 . As a result, the horizontal displacement of the first projectile at time t is v 1 t cos α 1 . Similarly, the horizontal displacement of the second projectile is v 2 t cos α 2 .
It is also known that the horizontal displacement of the two projectiles is the same, and they travel this distance at the same time. Thus v 1 T cos α 1 v 1 cos α 1 = v 2 T cos α 2 = v 2 cos α 2
Part 2:
Here, we will determine an expression for T .
We consider the first projectile, as it is easier to work with. To determine T , we need to determine when the projectile hits the ground again. y ¨ ⟹ y ˙ At t = 0 , y ˙ = v 1 sin α 1 ⟹ C ⟹ y ˙ ⟹ y At t = 0 , y = 0 ⟹ C ⟹ y At t = T , y ⟹ 0 ⟹ T = − g = − g t + C = v 1 sin α 1 = − g t + v 1 sin α 1 = − 2 1 g t 2 + v 1 t sin α 1 + C = 0 = − 2 1 g t 2 + v 1 t sin α 1 = 0 = T ( v 1 sin α 1 − 2 1 g T ) = g 2 v 1 sin α 1
Part 3:
We will determine an expression for d .
This specifically requires the usage of the first projectile. From Part 1, we have d = v 1 T cos α 1 = g 2 v 1 2 sin α 1 cos α 1
Part 4:
We will determine an expression for h .
This specifically requires the usage of the second particle. We have y ¨ ⟹ y ˙ At t = 0 , y ˙ = v 2 sin α 2 ⟹ C ⟹ y ˙ ⟹ y At t = 0 , y = 0 ⟹ C ⟹ y At t = T , y ⟹ h = − g = − g t + C = v 2 sin α 2 = − g t + v 2 sin α 2 = − 2 1 g t 2 + v 2 t sin α 2 + C = 0 = − 2 1 g t 2 + v 2 t sin α 2 = h = − 2 1 g ( g 2 v 1 sin α 1 ) 2 + v 2 ( g 2 v 1 sin α 1 ) sin α 2 = ( g 2 v 1 sin α 1 ) ( v 2 sin α 2 − v 1 sin α 1 )
Part 5:
We will now determine the angle subtended by the pole from P .
We will determine this using tangent results. tan α = d h = g 2 v 1 2 sin α 1 cos α 1 ( g 2 v 1 sin α 1 ) ( v 2 sin α 2 − v 1 sin α 1 ) = v 1 cos α 1 v 2 sin α 2 − v 1 sin α 1 = v 1 cos α 1 v 2 sin α 2 − v 1 cos α 1 v 1 sin α 1 = v 2 cos α 2 v 2 sin α 2 − v 1 cos α 1 v 1 sin α 1 using Part 1 = tan α 2 − tan α 1
Thus, we have an expression for the angle in terms of the other two angles. Therefore, we have derived the general expression.
Substituting the specific values gives us tan α = tan 6 0 ∘ − tan 3 0 ∘ = 3 − 3 1 ≈ 1 . 1 5 5 .
What I loved about this question was the obvious lack of available information, and how all the variables cancelled out in the end.
Oooh, really nice!
I like the general solution
did it the same way
In the third part, you can simplify g 2 v 1 2 sin α 1 cos α 1 to g v 1 2 sin ( 2 α 1 )
I'll tackle this problem using basic principles of classical mechanics.
Let the projectile which hits the foot of the pole be projectile 1 and the projectile which hits the top of the pole projectile 2 .
tan α = distance between P and foot of the pole height of the pole and thus in order to calculate tangent of alpha we will need height of the pole ( h ) and distance between P and foot of the pole ( d ).
If the velocity of projectile is υ , then let υ x be the velocity in horizontal direction and υ y velocity in vertical direction. Note that if two projectiles hit the pole at the same time, that means that they have both travelled the same horizontal distance and hence that their horizontal velocity components are equal - υ x .
It follows that:
tan 3 0 ∘ = υ x υ y 1 ⇒ υ x = 3 υ y 1 and
tan 6 0 ∘ = υ x υ y 2 ⇒ υ y 2 = 3 υ x and hence
υ y 2 = 3 υ y 1 .
Time needed for projectile 1 to reach max. height can be derived from following equation: υ y 1 − g t = 0 and it equals t = g υ y 1 (note that it will take twice as much for projectile to land and hit foot of the pole). Distance between the shooting spot and foot of the pole will be product of horizontal velocity and the time for which projectile lands again:
d = υ x × 2 t = g 2 υ x υ y 1 = g 2 3 υ y 1 2 .
In order to find height of the pole, we can integrate vertical speed of projectile 2 across interval ( 0 , 2 t ) what will eventually lead us to the well-known formula for distance travelled (just modified for our case):
h = υ y 2 × 2 t − 2 g × ( 2 t ) 2 = 2 υ y 2 t − 2 g t 2
→ t = g υ y 1
h = g 2 × υ y 1 × υ y 2 − g 2 υ y 1 2
→ υ y 2 = 3 υ y 1
h = g 6 υ y 1 2 − 2 υ y 1 2 = g 4 υ y 1 2 .
Finally, we have:
tan α = d h = g 2 3 υ y 1 2 g 4 υ y 1 2 = 3 2 ≈ 1 . 1 5 5 .
Because the 2 projectiles hit the vertical pole at the same time, we know that cos ( 3 0 o ) ⋅ v 1 ⋅ t = cos ( 6 0 o ) ⋅ v 2 ⋅ t , where v 1 represents the velocity of the bottom projectile and v 2 represents the velocity of the top projectile. Now, we solve this equation to find the relation between the 2 velocities: cos ( 3 0 o ) ⋅ v 1 ⋅ t = cos ( 6 0 o ) ⋅ v 2 ⋅ t 2 3 ⋅ v 1 = 2 v 2 3 ⋅ v 1 = v 2 . For simplicity, let v 1 = 1 . Now, we want to find the time when the first projectile hits the floor, so we get − 2 1 g t 2 + sin ( 3 0 o ) ⋅ 1 ⋅ t = 0 t ( − 2 1 g t + 2 1 ) = 0 − g t = − 1 ⟹ t = g 1 Now, all we need to do is calculate the height of the pole and its distance from point P . Let's start with the length cos ( 3 0 o ) ⋅ t = 2 3 ⋅ g 1 = 2 g 3 And then the height: − 2 1 g t 2 + sin ( 6 0 o ) ⋅ v 2 ⋅ t − 2 1 g ⋅ ( g 1 ) 2 + 2 3 v 2 ⋅ g 1 − 2 g 1 2 + 2 3 ⋅ 3 ⋅ 1 ⋅ g 1 2 g 2 ⋅ 1 2 = g 1 , So tan ( α ) = 2 g 3 g 1 = 3 2 ≈ 1 . 1 5 5
We shall be using the equation of a projectile : y = x tan θ ( 1 − R x ) . You can find a proof under this section of the wiki on projectile motion.
Let the green projectile (launched at 6 0 ∘ ) be P 1 and the blue one (launched at 3 0 ∘ )be P 2 . Also let the height of the pole be h . Now, observe that since both take an equal amount of time to travel the same distance in the horizontal direction,
V x 1 = V x 2 ⇒ V 1 = V 2 3
as V x = V cos θ . Also, since P 2 hits the bottom of the pole, it's range ( R 2 )is the side adjacent to α .
R 2 = g V 2 2 sin ( 3 π ) = 2 3 g V 1 2 , R 1 = g V 1 2 sin ( 3 2 π ) = 2 g V 1 2 3
When P 1 hits the top of the pole, x = R 2 .
∴ y = h = 2 3 g V 1 2 tan 3 π ⋅ ( 1 − R 1 R 2 ) = 2 g V 1 2 ( 3 2 ) = 3 g V 1 2
So we can conclude that,
tan α = R 2 h = 3 2 ≈ 1 . 1 5 5
Strategy : Get rid of gravitation by using a local intertial frame. The problem then becomes linear!
View the situation from a free-fall perspective, where the "camera" starts falling from rest at the moment the projectiles are launched. In this frame of reference there is no gravitational acceleration, and the projectiles travel in a straight line at constant velocity. The situation then looks like this: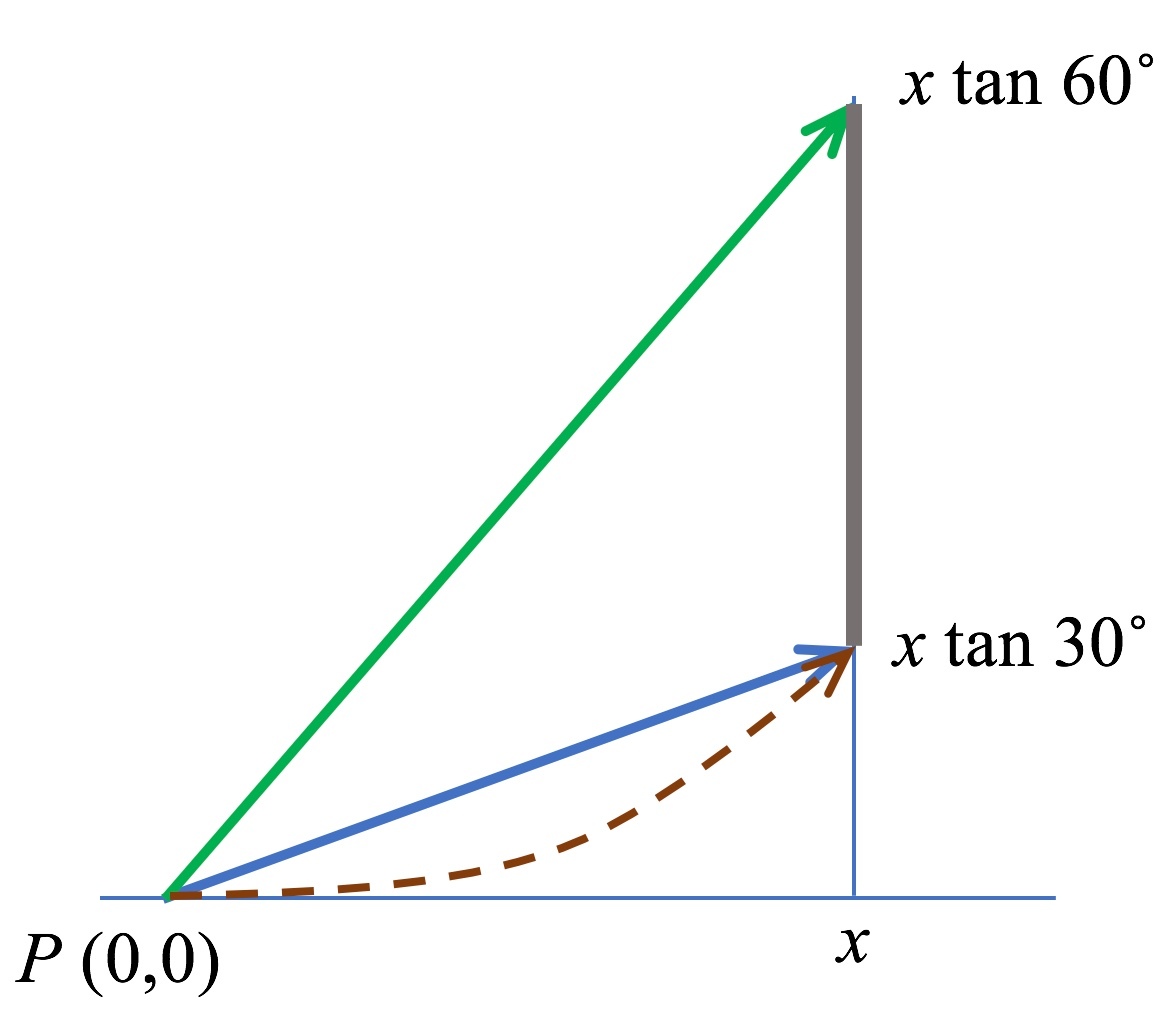
(The brown dashed line indicates the accelerated motion of the ground in our frame of reference.)
We see immediately that the length of the pole is x tan 6 0 ∘ − x tan 3 0 ∘ , so that tan α = x x tan 6 0 ∘ − x tan 3 0 ∘ = tan 6 0 ∘ − tan 3 0 ∘ = 3 − 3 1 = 3 2 , making the answer 1 . 1 5 5 . This corresponds to an angle of about 4 9 ∘ .
Alternative solution in the original frame of reference:
Let v x be the horizontal velocity component of the projectiles; we know that it remains constant and is equal for both projectiles. The initial vertical velocity component is then v y = v x tan θ , where θ is the launch angle. The equations of motion are x ( t ) = v x t ; y ( t ) = v x t tan θ − 2 1 g t 2 . Let t ⋆ be the time of impact, x ⋆ the horizontal distance traveled at that time, and y θ ⋆ the height of the projectile at that time. Then clearly x ⋆ = v x t ⋆ ; y θ ⋆ = x ⋆ tan θ − 2 1 g ( t ⋆ ) 2 . From y 3 0 ∘ ⋆ = 0 it follows that 2 1 g ( t ⋆ ) 2 = x ⋆ tan 3 0 ∘ ; and the height of the pole is y 6 0 ∘ ⋆ = x ⋆ tan 6 0 ∘ − 2 1 g ( t ⋆ ) 2 = x ⋆ tan 6 0 ∘ − x ⋆ tan 3 0 ∘ . Finally, tan α = x ⋆ y 6 0 ∘ ⋆ = x ⋆ x ⋆ tan 6 0 ∘ − x ⋆ tan 3 0 ∘ = tan 6 0 ∘ − tan 3 0 ∘ .