Not enough information? Do some construction!
Let A B C be an isosceles triangle with ∠ A B C = ∠ A C B = 8 0 ∘ . Point M is on side A B (not on A B extended) such that A M = B C . Find ∠ M C B in degrees.
The answer is 70.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
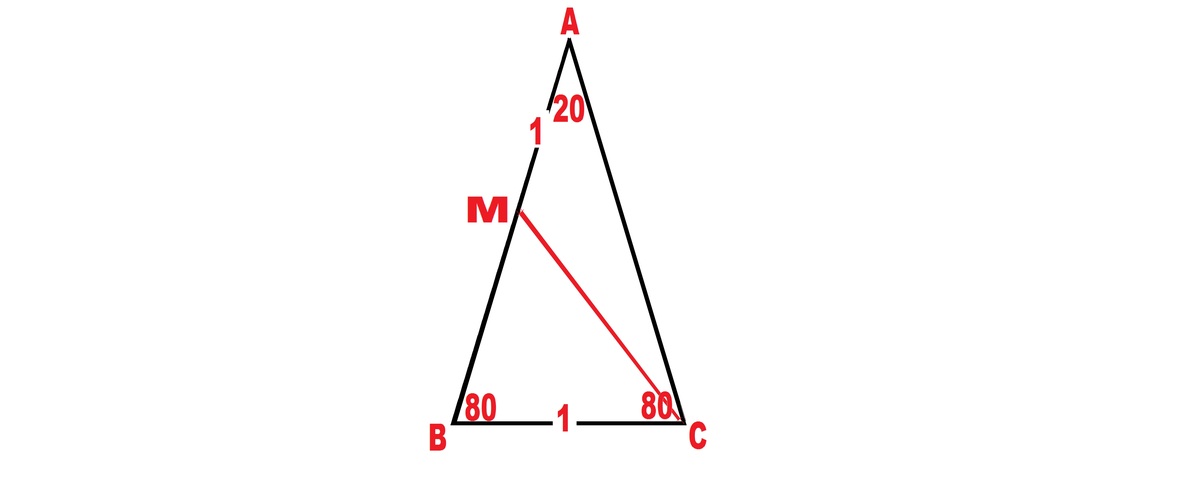
Without loss of generality let BC=1. Applying Sin Law to triangle ABC we get S i n 2 0 B C = S i n 8 0 A B . A B = 2 . 8 7 9 3 8 . ∴ M B = 1 . 8 7 9 3 8 . I n Δ M B C , A p p l y i n g C o s L a w , M C 2 = 1 . 8 7 9 3 8 2 + 1 2 − 2 ∗ 1 . 8 7 9 3 8 ∗ 1 ∗ C o s 8 0 , ∴ M C = 1 . 9 6 9 6 . A p p l y i n g S i n L a w , 1 . 8 7 9 3 8 S i n M C B = 1 . 9 6 9 6 S i n 8 0 . ∴ ∠ M C B = 7 0 o .
why do you let BC be 1 and how does this not effect the question in a negative way?
Log in to reply
Because the length is arbitrary. Scaling all lengths the same leaves the angles invariant, so you might as well just set the one unknown length to 1
Log in to reply
ok thank you
Thank you. It also simplifies calculations.
Nice construction! What software is that?
I hope it is clear enough, it is only 2 equations, but a calculator is needed to get the final number.
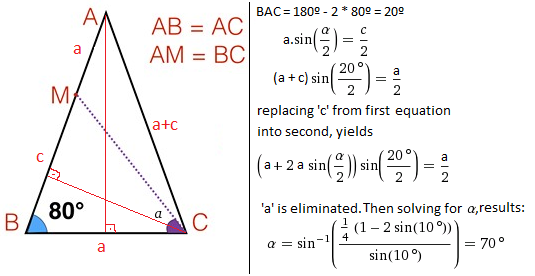

Image from GeoGebra .
Motivation for construction: A M = B C means that we would want to "move" a shape with base A M (probably a triangle) to B C .
Hence we have point D such that △ B C D ≡ △ A M C .
By construction, B D = A C = A B , thus △ A B D is an isosceles triangle.
Also, ∠ M A C = 1 8 0 ∘ − 2 ∗ 8 0 ∘ = 2 0 ∘ ⇒ ∠ A B D = 8 0 ∘ − 2 0 ∘ = 6 0 ∘
Hence △ A B D is an equilateral triangle.
Furthermore, note that A D = B D = A C , so △ A C D is isosceles.
∠ C A D = 6 0 ∘ − 2 0 ∘ = 4 0 ∘ ⇒ ∠ A D C = 2 1 8 0 ∘ − 4 0 ∘ = 7 0 ∘ ⇒ ∠ A C M = ∠ B D C = 7 0 ∘ − 6 0 ∘ = 1 0 ∘
Finally, ∠ M C B = 8 0 ∘ − 1 0 ∘ = 7 0 ∘