Not just trigonometry, its graph theory
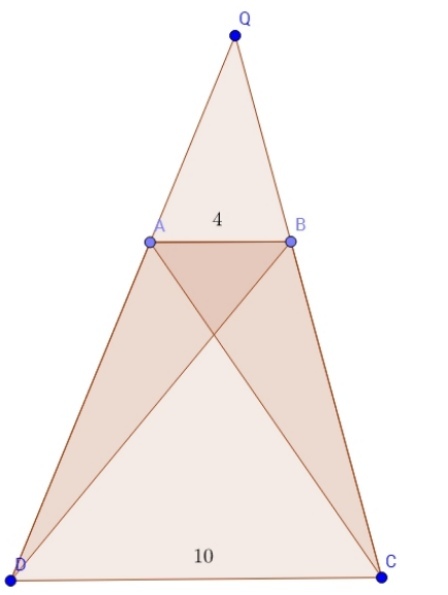
Let be a trapezoid with with side lengths shown above. . and intersect at right angles.
Find the area of .
Give your answer to 3 decimal places.
The answer is 46.666.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the point of intersection of AC and BD be E .
△ABE and △CDE are similar , so AE = (2/5)CE and BE = (2/5)DE .
△AED is a right triangle , so AD^2 = AE^2 + DE^2 = (4/25)CE^2 + DE^2 .
△BEC is a right triangle , so BC^2 = BE^2 + CE^2 = (4/25)DE^2 + CE^2 .
So AD^2 + BC^2 = (29/25)CE^2 + (29/25)DE^2 .
△CED is a right triangle ,
CE^2 + DE^2 = CD^2 = 100
(29/25)CE^2 + (29/25)DE^2 = (29/25)*100 = 116
So AD^2 + BC^2 = 116 .
We know △AQB and △DQC are similar ,
QD = (5/2)QA , so
AD = QD - QA = (3/2)QA
QC = (5/2)QB , so
BC = QC - QB = (3/2)QB
Therefore
[(3/2)QA]^2 + [(3/2)QB]^2 = 116
(9/4)QA^2 + (9/4)QB^2 = 116
QA^2 + QB^2 = 464/9
Use cosine law for △AQB ,
AB^2 = QA^2 + QB^2 - 2QA QB cos45°
16 = 464/9 - 2QA QB (1/√2)
(√2)QA*QB = 464/9 - 16 = 320/9
QA*QB = (320/9) / √2 = 320/(9√2)
Let the area of △QAB be Area(△QAB) ,
Area(△QAB) = (1/2) QA QB*sin45°
= 160/(9√2)*(1/√2)
= 80/9
Let the area of △QDC be Area(△QDC) ,
Area(△QDC) = [(5/2)^2]Area(△QAB)
= (25/4)*(80/9)
= 500/9
So the area of the trapezoid ABCD is Area(△QDC) - Area(△QAB) = 420/9 = 140/3 .