Not Just Vieta's Derivatives!
P ( x ) Q ( x ) = = x 6 − x 5 − x 3 − x 2 − x x 4 − x 3 − x 2 − 1
Consider the polynomials above.
Given that z 1 , z 2 , z 3 , and z 4 are the roots of Q ( x ) = 0 , find P ( z 1 ) + P ( z 2 ) + P ( z 3 ) + P ( z 4 ) .
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
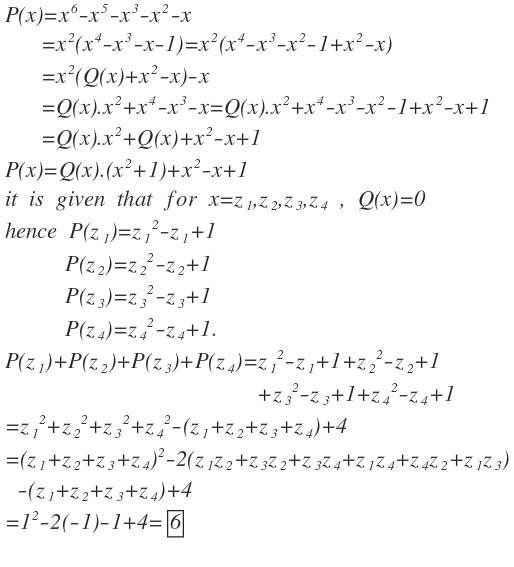
Same method+1
Same method but I used Newton's sums.
U stole my method U thief. I will not leave U. Joking xD. Great Job !
P(x)=x^2(x^4-x^3-x-1)-x
P(x)=x^2(x^2-x)-x
P(x)=x^4-x^3-x
P(x) = x^2-x+1
In various places I have substituted x^4-x^3=x^2+1 as Q(x) is zero.
Now sum of squares of roots of Q(x)=3
Sum if roots =1
Hence answer = 3-1+4=6.
This is the simplest approach i have .
So isn't the answer 3? 3 -1 + 1? Where did you get that 4 there in the last equation?