Not L'Hôpital's Rule

Calculus Level 5

Let $f(x)=a+e^{bx}$ and $g(x)=c+e^{dx}$ . Consider the following statement:

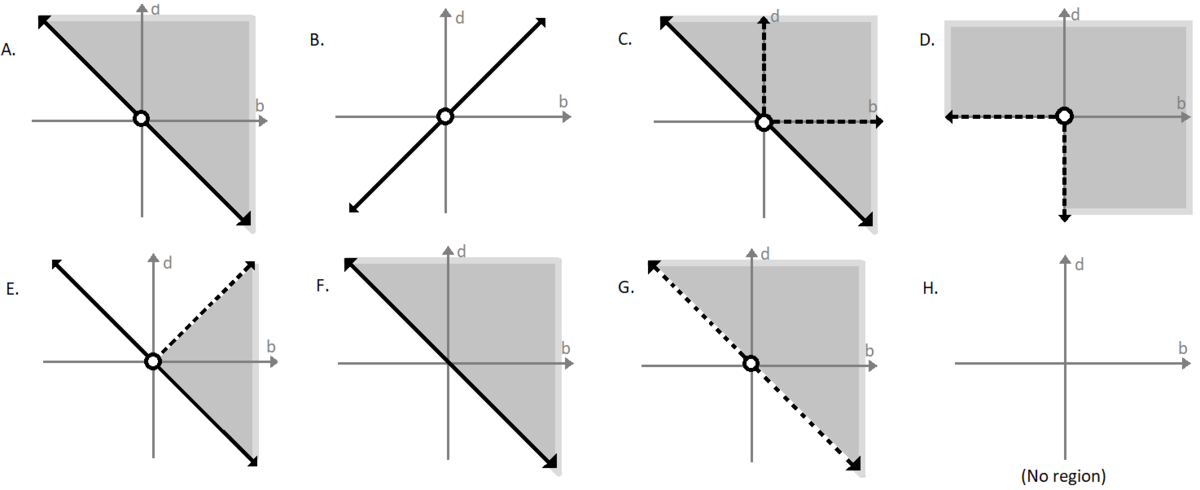
$\lim\limits_{x\rightarrow \infty} f(x) g(x)=\lim\limits_{x\rightarrow \infty}f'(x) g'(x)$ .

Which of the graphs below shows the region of the real $bd$ plane for which there are no real values of $a$ and $c$ that would make the statement true?

Regions include shaded areas as well as solid black lines or points on the graph. Dotted lines and open circles (denoting the point at the center of the circle) are excluded from the region.

G H C E D F B A

1 solution

Eric Nordstrom
Jul 1, 2019

The statement can be expanded as follows:

$\lim\limits_{x\rightarrow \infty}\left[ac+ce^{bx}+ae^{dx}+e^{(b+d)x}\right]=\lim\limits_{x\rightarrow \infty}bde^{(b+d)x}$ .

The behavior of each exponential term can be separated into three categories of the coefficient in the exponent:

Negative: The term will go to zero.
Zero: The term equals the coefficient in front of it.
Positive: The term goes to $\pm \infty$ unless the coefficient in front of it is zero. The term can also be canceled out by other terms with the same exponent if the coefficients preceding all these terms sum to zero. For example, $\lim\limits_{x\rightarrow \infty}\left[(0)e^x+(1)e^{2x}+(-1)e^{2x}\right]=0$ .

There are two ways to have no solution to the statement of interest:

One or both of the limits do not exist. (Note that $\infty=\infty$ and $-\infty=-\infty$ are not considered true statements.)
The limits both exist, but there is no real solution to the equation that results from evaluating them.

In the first case, we cannot simply check whether a term goes to $\pm \infty$ because it could be canceled out by another term. In the second case, we cannot simply check whether the limits are finite because we still have to solve the equation. Therefore, we have to check every case of positive, negative, and zero. Specifically, we have to check cases for each of the exponential coefficients $b$ , $d$ , and their sum $b+d$ , whose sign is undetermined if $b$ and $d$ have opposite sign. In each case, we must determine the conditions under which there can be a solution. If the conditions do not conflict, then there is a solution in that case. For convenience, the conditions can be placed in the following categories:

ensuring that no terms go to $\pm \infty$ so that the limits exist
solving the equation that results, assuming no terms to go $\pm \infty$

Here is the analysis of each case:

b	d	b + d	Ensuring limits exist	Equation	Conclusion
-	-	-	N/A	$ac=0$	$a=0$ or $c=0$
-	0	-	N/A	$ac+a=a(c+1)=0$	$a=0$ or $c=-1$
-	+	-	$a=0$	$ac=0$	$a=0$
-	+	0	$a=0$	$ac+1=bd$	No solution: $ac+1=(0)c+1=1$ but $bd<0$ since $b$ and $d$ have opposite sign, so $bd$ cannot equal 1 and the conditions therefore conflict.
-	+	+	$a=0$ and $1=0$ (false) and $bd=0$ (false) or $d=b+d$ (false) and $a+1=0$ and $bd=0$ (false)	$ac=0$	No solution: There is no way to make the limits exist.
0	-	-	(symmetry)	(symmetry)	By symmetry from (-, 0, -) case: $a=-1$ or $c=0$
0	0	0	N/A	$ac+c+a+1=(a+1)(c+1)=0$ and $bd=0$ (true)	$a=-1$ or $c=-1$
0	+	+	$a=0$ and $1=0$ (false) and $bd=0$ (true) or $d=b+d$ (true) and $a+1=0$ and $bd=0$ (true)	$ac+c=(a+1)c=0$	$a=-1$
+	-	-	(symmetry)	(symmetry)	By symmetry from (-, +, -) case: $c=0$
+	-	0	(symmetry)	(symmetry)	By symmetry from (-, +, 0) case: No solution.
+	-	+	(symmetry)	(symmetry)	By symmetry from (-, +, +) case: No solution.
+	0	+	(symmetry)	(symmetry)	By symmetry from (0, +, +) case: $c=-1$
+	+	+	$c=0$ and $a=0$ and $1=0$ (false) and $bd=0$ (false) or $b=d$ and $1=0$ (false) and $bd=0$ (false) and $c+a=0$ or $b=b+d$ (false) and $a=0$ and $bd=0$ (false) and $c+1=0$ or $d=b+d$ (false) and $c=0$ and $bd=0$ (false) and $a+1=0$ or $b=d=b+d$ (false) and $bd=0$ (false) and $c+a+1=0$	ac=0	No solution: There is no way to make the limits exist.

The final answer is the union of cases of +/-/0 in which there is no solution:

b	d	b + d	Description
-	+	0	The line $b+d=0$ ( $d=-b$ ), left of the origin.
-	+	+	Above the line $d=-b$ , left of the origin.
+	-	0	The line $d=-b$ , right of the origin.
+	-	+	Above the line $d=-b$ , below the origin.
+	+	+	Quadrant I

Great work ! Checking all theses cases is not an easy task ! But maybe you should specify that $+\infty=+\infty$ is not a true statement.

Théo Leblanc - 1 year, 8 months ago

Thanks Theo! I think I did mention that? Or did you mean specifically using the + signs?

Eric Nordstrom - 1 year, 8 months ago

Yes you specify it in the solution but not in the problem itself, in a lot of theories considering $+\infty=+\infty$ as a true statement is very useful and that's the point of my remark.

Théo Leblanc - 1 year, 7 months ago

PS: I use + because it is common in France ( yes in English it is implicit )

Théo Leblanc - 1 year, 7 months ago

Ah. Yes, but I think I left out the option where $\infty = \infty$ is true. Interesting about the explicit "+" in France!

Eric Nordstrom - 1 year, 5 months ago

Not L'Hôpital's Rule

1 solution

0 pending reports