Not Me!

Probability Level 4

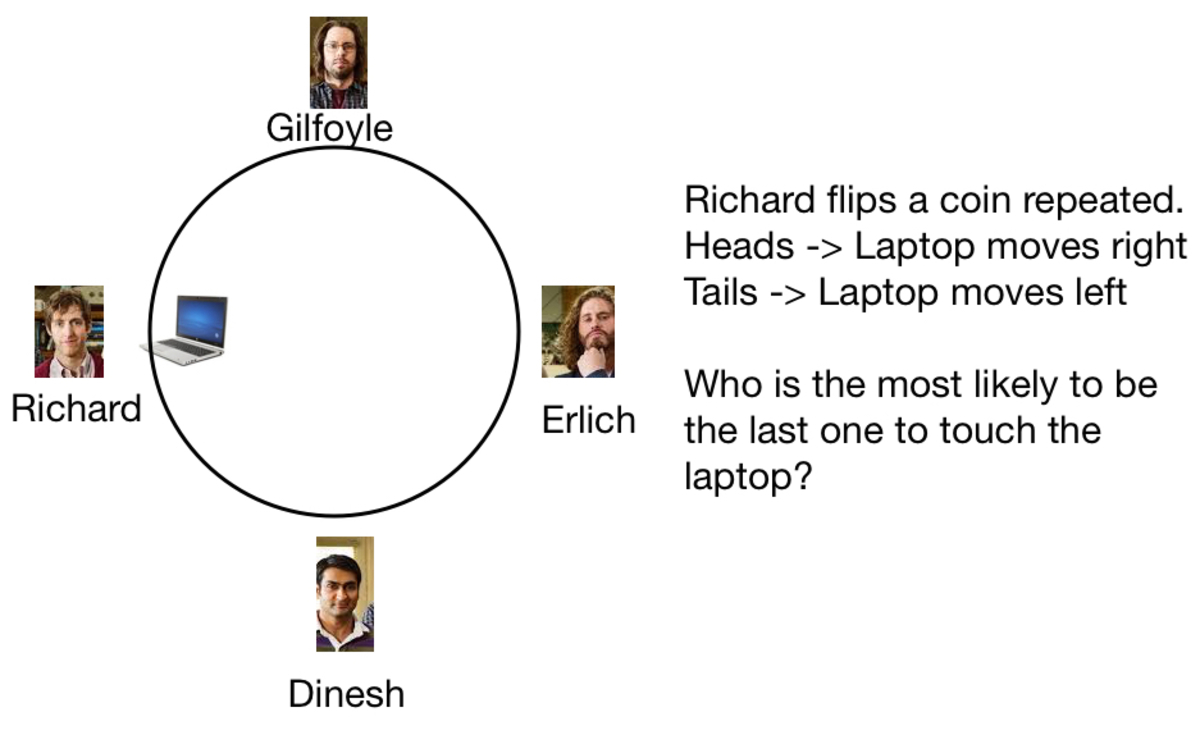
4 people, Richard, Dinesh, Erlich and Gilfoyle (in that order) sit around a desk. They have to code up a project on a laptop that Richard holds. Richard decides that he will pass a laptop around the table by flipping a coin repeatedly. If the coin lands on Heads, then the laptop moves to the right. If the coin lands on Tails, then the laptop moves to the left. The person who has to code up the project is the last person in the team who has touched the laptop.

Who is most likely to have to code up the project?

Note: Richard has touched the laptop at the start.

Dinesh or Gilfoyle, equally Gilfoyle Dinesh, Erlich or Gilfoyle, equally Dinesh Erlich

Calvin Lin by Calvin Lin

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Michael Mendrin
Jul 26, 2016

Let the coders be R , G , E , D R, G, E, D , where R R has the laptop and therefore will not be the last to touch it. The next to touch the laptop are G , D G, D with equal probability. Let's look at the case where G G gets the laptop. Then the probability of either E E or D D being the 3 3 rd to touch it are, respectively

∑ n = 0 ∞ 1 2 2 n + 1 = 2 3 \displaystyle \sum _{ n=0 }^{ \infty }{ \dfrac { 1 }{ { 2 }^{ 2n+1 } } } =\dfrac { 2 }{ 3 }
∑ n = 1 ∞ 1 2 2 n = 1 3 \displaystyle \sum _{ n=1 }^{ \infty }{ \dfrac { 1 }{ { 2 }^{ 2n } } } =\dfrac { 1 }{ 3 }

which means that the probability that E E or D D ends up being the last to touch the laptop are, respectively

1 2 ⋅ 1 3 \dfrac{1}{2}\cdot \dfrac{1}{3} and 1 2 ⋅ 2 3 \dfrac{1}{2}\cdot \dfrac{2}{3}

In the case where D D is the 2 2 nd person to get the laptop, the probability that E E or G G ends up being the last to touch the laptop are, respectively

1 2 ⋅ 1 3 \dfrac{1}{2}\cdot \dfrac{1}{3} and 1 2 ⋅ 2 3 \dfrac{1}{2}\cdot \dfrac{2}{3}

so that the probabilities of G , E , D G, E, D being the one to code up the project are, respectiviely

1 2 ⋅ 0 + 1 2 ⋅ 2 3 = 1 3 \dfrac { 1 }{ 2 } \cdot 0 +\dfrac { 1 }{ 2 }\cdot \dfrac { 2 }{ 3 } =\dfrac { 1 }{ 3 }
1 2 ⋅ 1 3 + 1 2 ⋅ 1 3 = 1 3 \dfrac { 1 }{ 2 }\cdot \dfrac { 1 }{ 3 } +\dfrac { 1 }{ 2 }\cdot \dfrac { 1 }{ 3 } =\dfrac { 1 }{ 3 }
1 2 ⋅ 0 + 1 2 ⋅ 2 3 = 1 3 \dfrac { 1 }{ 2 }\cdot 0 +\dfrac { 1 }{ 2 }\cdot \dfrac { 2 }{ 3 } =\dfrac { 1 }{ 3 }

2 Helpful 0 Interesting 0 Brilliant 0 Confused

Great. The 4-people case is easy to analyze numerically. What about the n n -people case? What can we say about their probabilities​?

Calvin Lin Staff - 4 years, 10 months ago

Log in to reply

Would like to know! :D

Aniket Sanghi - 4 years, 10 months ago

In fact, in the general case of n-people, curiously the probability remains the same for everybody. Kind of counter-intuitive. When I get the time, if nobody else will, I'll try to post the general solution. You're right, the 4-people case is easy to analyze numerically.

Michael Mendrin - 4 years, 10 months ago

Thanks for the sol :)

Aniket Sanghi - 4 years, 10 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...