Not ordinary equations!

Rewrite the equations as: $\begin{aligned} a^2+b^2-2ab\cos(120^\circ)=3^2 \quad ... \quad &(1) \\ b^2+c^2-2bc\cos(120^\circ)=\sqrt{52}^2 \quad ... \quad &(2) \\ c^2+a^2-2ca\cos(120^\circ)=7^2 \quad ... \quad &(3) \end{aligned}$

By law of cosines and the fact that the three angles add up to $360^\circ$ , we can construct the following triangle: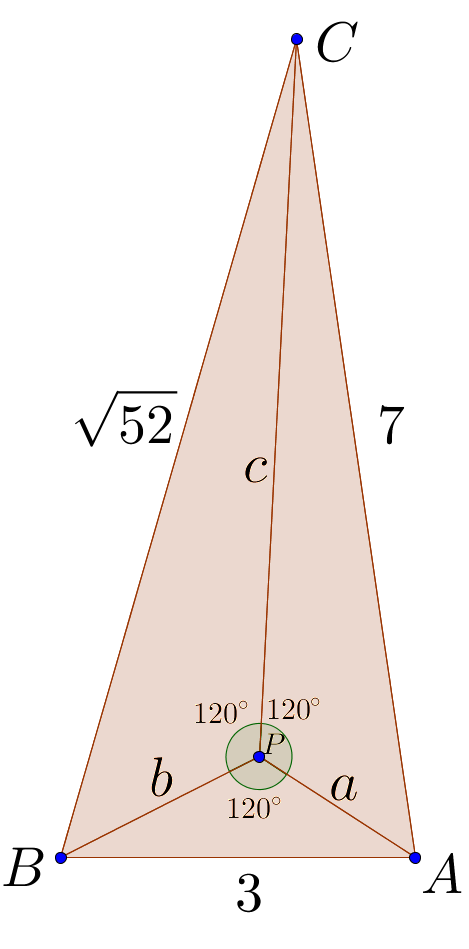 By Heron's formula, the total area is $[ABC]=6\sqrt{3}$ . Now, considering the small triangles and adding their areas we also get $[ABC]=(ab+bc+ca)\frac{\sin(120^\circ)}{2}$ , then:

$ab+bc+ca=\pm 24 \quad ... \quad (4)$ (see why it can also be negative and how the triangle changes).

By adding $(1),(2)$ and $(3)$ we get $2(a^2+b^2+c^2)+ab+bc+ca=110$ , and use $(a+b+c)^2=a^2+b^2+c^2+2(ab+bc+ca)$ to get $2(a+b+c)^2-3(ab+bc+ca)=110$ . Replace the value of $(4)$ to get:

$a+b+c=\color{#3D99F6}{\pm}\sqrt{55\pm 36} \quad ... \quad (5)$

Ssubtract $(2)$ from $(1)$ to get with $(5)$ :

$(a+b+c)(a-c)=-43 \implies c=a\color{#3D99F6}{\pm}\dfrac{43}{\sqrt{55\pm 36}} \quad ... \quad (6)$

Similarly, subtract $(3)$ from $(2)$ :

$(a+b+c)(b-a)=3 \implies b=a\color{#3D99F6}{\pm}\dfrac{3}{\sqrt{55\pm 36}} \quad ... \quad (7)$

Substitute $(6)$ and $(7)$ in $(5)$ :

$3a\color{#3D99F6}{\pm}\dfrac{46}{\sqrt{55\pm 36}}=\color{#3D99F6}{\pm}\sqrt{55\pm 36} \implies a=\color{#3D99F6}{\pm}\dfrac{(55\pm 36)-46}{3\sqrt{55\pm 36}}$

Find $b$ and $c$ :

$b=\color{#3D99F6}{\pm}\dfrac{(55\pm 36)-37}{3\sqrt{55\pm 36}}$

$c=\color{#3D99F6}{\pm}\dfrac{(55\pm 36)+83}{3\sqrt{55\pm 36}}$

We get four solutions combining the $\color{#3D99F6}{\pm}$ and the $\pm$ signs: $(a,b,c)=\left(\frac{15}{\sqrt{91}},\frac{18}{\sqrt{91}},\frac{58}{\sqrt{91}}\right)$ , $\left(-\frac{15}{\sqrt{91}},-\frac{18}{\sqrt{91}},-\frac{58}{\sqrt{91}}\right)$ , $\left(-\frac{9}{\sqrt{19}},-\frac{6}{\sqrt{19}},\frac{34}{\sqrt{19}}\right)$ , $\left(\frac{9}{\sqrt{19}},\frac{6}{\sqrt{19}},-\frac{34}{\sqrt{19}}\right)$

Only the last two pairs give us an integer value for the asked expression, so:

$\dfrac{49b^2+39bc+9c^2}{a^2}=\dfrac{49(6)^2+39(6)(-34)+9(-34)^2}{9^2}=\dfrac{4212}{81}=\boxed{52}$ .