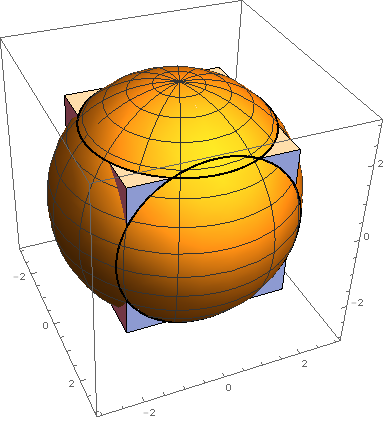
Not quite 1 8 0 ∘ ? - Inpsired by Otto Bretscher's Intriguing Ornament
Consider a sphere of diameter 6 cm and a concentric cube of side length 4 cm . What is the sum of the angles, θ s , in a triangle on the sphere defined by an intersection of the cube and the sphere? Give your answer, θ s , in degrees, rounded to the nearest integer.
The answer is 111.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Great solution to a great problem, Comrade! This would have been a great problem on the third or fourth homework set in our vector calculus class, when we were talking about tangent trajectories.
I did it in essentially the same way, finding the angle θ between the parameterized circles ( 2 , 5 cos t , 5 sin t ) and ( 5 cos t , 2 , 5 sin t ) at the point ( 2 , 2 , 1 ) . The velocity vectors are v = ( 0 , − 5 sin t , 5 cos t ) = ( 0 , − 1 , 2 ) and w = ( − 5 sin t , 0 , 5 cos t ) = ( − 1 , 0 , 2 ) and cos θ = ∣ ∣ v ∣ ∣ ∣ ∣ w ∣ ∣ v ⋅ w = 5 4 , as you said.
This in, in fact, the same solution as the others. I just set up the commands that drew the picture so that the answer could be derived directly from the contents of the command.

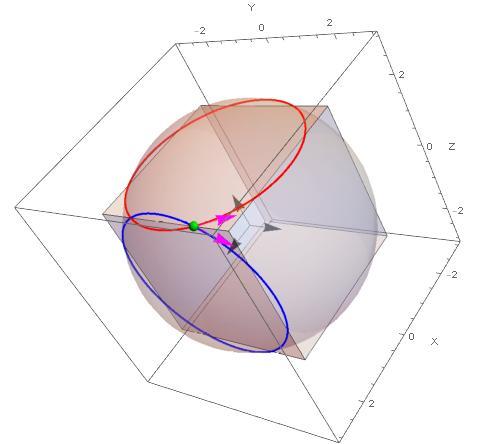
The red and blue circles form two side of the angle, The green small sphere (a point) is at the vertex of the angle.
The dot product of the two 3D tangent vector gives the cosine of the angle as 5 4 as mentioned by the others.
∘ N [ 3 cos − 1 ( 5 4 ) ] is 1 1 0 . 6 0 9 6 9 2 9 3 8 o .
Here is an orienting drawing:
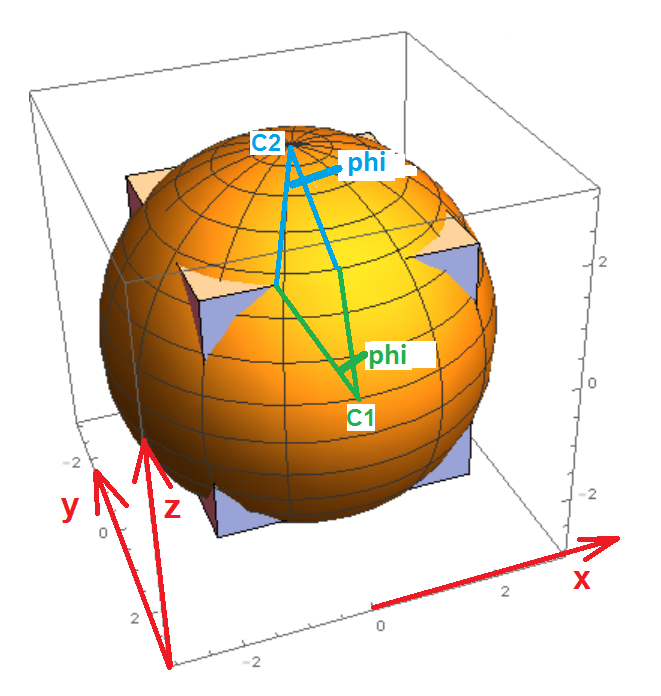
Consider two circles; one at z = 2 and one at y = − 2 . The circles have diameters which area larger than the cube side length. Find the radius of the circles:
2 2 + r 2 = 3 2 r = 5
Coordinates of the circle centers: C 1 = ( 0 , − 2 , 0 ) C 2 = ( 0 , 0 , 2 )
Find the angle ϕ such that the two circles intersect (refer to the diagram):
C 2 y − r c o s ϕ = C 1 y − r c o s ϕ = − 2 ϕ = a c o s ( 5 2 )
The intersection point of the two circles is:
P x = C 1 x − r s i n ϕ P y = C 1 y P z = C 1 z + r c o s ϕ
Now suppose we go a bit farther on each circle by an infinitesimal amount ϵ . These other two points are:
Q x = C 1 x − r s i n ( ϕ + ϵ ) Q y = C 1 y Q z = C 1 z + r c o s ( ϕ + ϵ ) R x = C 2 x − r s i n ( ϕ + ϵ ) R y = C 2 y − r c o s ( ϕ + ϵ ) R z = C 2 z
Calculate two vectors:
v 1 = Q − P v 2 = R − P
Per the dot product formula:
v 1 ⋅ v 2 = ∣ v 1 ∣ ∣ v 2 ∣ c o s ( 3 θ ) θ = 3 a c o s ( ∣ v 1 ∣ ∣ v 2 ∣ v 1 ⋅ v 2 )
Taking the limit of the θ expression as ϵ tends toward zero yields θ ≈ 1 1 1 ∘
Thanks, @Steven Chase , for an interesting approach!
Congrats to your first problem, Comrade; a good one indeed!
Sadly, my busy schedule does not allow me to write a solution at this time; let's just mention that the answer is 3 arccos ( 5 4 ) ≈ 1 1 1 ∘ . I'm sure you will draw a beautiful picture to explain.
Update the next morning:
Let's find the angle θ between the parameterized circles ( 2 , 5 cos t , 5 sin t ) and ( 5 cos t , 2 , 5 sin t ) at the point ( 2 , 2 , 1 ) . The velocity vectors are v = ( 0 , − 5 sin t , 5 cos t ) = ( 0 , − 1 , 2 ) and w = ( − 5 sin t , 0 , 5 cos t ) = ( − 1 , 0 , 2 ) , so cos θ = ∣ ∣ v ∣ ∣ ∣ ∣ w ∣ ∣ v ⋅ w = 5 4 . Now we need three of those.
This is very similar in spirit to Cde Huan's excellent solution, of course.
Thanks Otto, for the solution and inspiration. Quite a gentle one to start, but at least somewhat original.
Log in to reply
Not that gentle, I suspect; let's see how many solvers you get.
@Otto Bretscher has provided a key step, while @Steven Chase has beaten me to a very careful solution. But here goes my (hopefully more simple) solution:
This problem boils down to finding the angle between two vectors in R 3 . From Figure 2, we find that the vectors are simply the tangent vectors to the "latitude" lines, defined by a face of the cube and the sphere. With a bit of geometry work (see Figure 1), we find that such two vectors are a = ( 0 , sin arccos 5 2 , 5 2 ) ∝ ( 0 , 1 , 2 ) and b = ( − sin arccos 5 2 , 0 , 5 2 ) ∝ ( − 1 , 0 , 2 ) . Note that we don't have to worry about their magnitudes - only directions matter!
So, a ⋅ b = cos θ i = 5 4 . By symmetry, θ s = 3 θ i = 3 arccos 5 4 . The answer we seek is θ s ≈ 1 1 1 ∘ .
Figure 1: The circle of radius 5 is "taken out" from the 3D figure below (Figure 2). The tangent vector is found by locating the point of intersection: y = 2 and r ′ = 5 . It is not hard to show that the tangent vector is proportional to ( 0 , 1 , 2 ) . Similarly, we can find the other vector.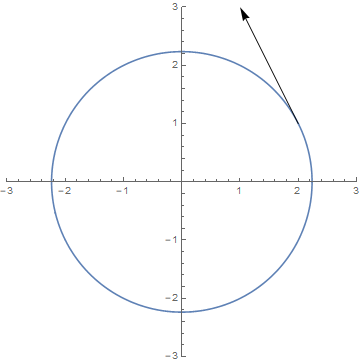
Figure 2: