Cosine of an inverse tangent

Geometry Level 1

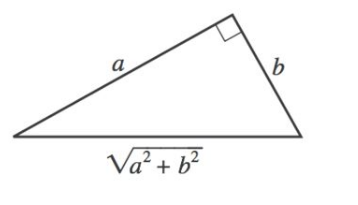
In the right triangle above, 0 < b < a 0<b<a . One of the angle measures in the triangle is tan ⁡ − 1 ( a b ) \tan^{-1} \left( \dfrac ab\right) . What is cos ⁡ [ tan ⁡ − 1 ( a b ) ] \cos \left[ \tan^{-1} \left( \dfrac ab\right) \right ] ?

a a 2 + b 2 \frac a{\sqrt{a^2+b^2}} a 2 + b 2 a \frac {\sqrt{a^2+b^2}}a b a 2 + b 2 \frac b{\sqrt{a^2+b^2}} a b \frac ab b a \frac ba

Hi Hi by Hi Hi , 18, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Hi Hi
Jun 30, 2016

If you remember your trigonometry rules, you know that tan − 1 a b \frac{a}{b} is the same as saying tanΘ = a b \frac{a}{b} . Knowing our mnemonic device SOH, CAH, TOA, we know that tan Θ = opposite/adjacent. If a is our opposite and b is our adjacent, this means that Θ will be our right-most angle.

Knowing that, we can find the cos of Θ as well. The cosine will be the adjacent over the hypotenuse. the adjacent still being b and the hypotenuse being √a2+b2. So cos[tan − 1 a b \frac{a}{b} ] will be:

b √ a 2 + b 2 \frac{b}{√a2+b2}

Our final answer is... b √ a 2 + b 2 \frac{b}{√a2+b2}

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...