Not so Simple 2
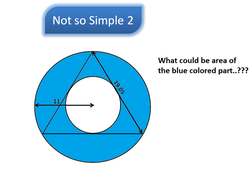 There are two circle and a equilateral triangle.
There are two circle and a equilateral triangle.
Big circle has radius of 11 and triangle has side of 19.05 as stated in the picture.
What could be area of the blue highlighted part..??
Round off final figure completely to avoid any mismatch.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
We know that perpendicular(height) of an equilateral triangle is also its median.Now center of the smaller circle is also the centroid of the triangle,This means it'll divide the height in 2:1,that means 1/3 of the height will be smaller circle's radius.Now the height of the triangle is (19.05 sin 60)=16.4977,1/3 of it 16.4977/3=5.499.So the blue shaded area=pi (R^2-r^2)=22/7 * 90.758=285.2398
first of all, it will be 14.xxxx not 1.4xxxx and , you can use the same median-centroid property in the second step as well, i.e Let the height of triangle be 3m, this implies that the centre of smaller circle divides it into 2:1 i.e 2m and 1m resp. Now, 2m part is the radius of bigger circle which implies that 2m=11 or simply m=5.5 Just subtract the area of smaller circle from area of bigger circle and you get the answer now.
Just a shorter solution, the bigger circle has a radius of 11 and the smaller one has a radius of 1 1 / 2 . The simplist way to proceed from here is to do difference of squares. ( 1 1 − 2 1 1 ) ( 1 1 + 2 1 1 ) = ( 2 1 1 ) ( 2 3 3 ) = 4 3 6 3 . The final step is to simply multiply this by pi
Radius of the in-circle is equal to the area divided by the semiperimeter. Then it's just a simple problem with two areas.
First of all we will find area of the big circle. Which is Pi * r ^ 2.
So area of big circle would be 3.142 * 11 ^ 2 = 380.1327.
Now see that there is an equilateral triangle. First we will find its height
Height of equilateral triangle h = side * sqrt (3) / 2.
h = 19.05 * sqrt (3) / 2 = 16.4977.
Now from the height of this circle we can find radius of the small circle. Which is 1/3 of h. So radius will be 1/3 * 16.4977 = 5.4992.
Now find area of small circle.
= 3.142 * 5.4992 ^ 2 = 95.0077.
Now just deduct area of small circle form the big one.
= 380.1327 - 95.0077 = 285.1251.
Rounding off completely we get area of 285.
If the outer radius is R and the inner radius is r, then the area of the highlighted part is = π(R^2-r^2). Using Pythagorean Theorem, we get (R^2-r^2)=(19.05/2)^2 Thus, The area= π(19.05/2)^2=285.022957 rounds up to 285
length of the side of the equilateral triangle was an extra info. just use the properties of circumcircle and incircle of an equilateral triangle :P
 side
side