Is this related to Kepler?
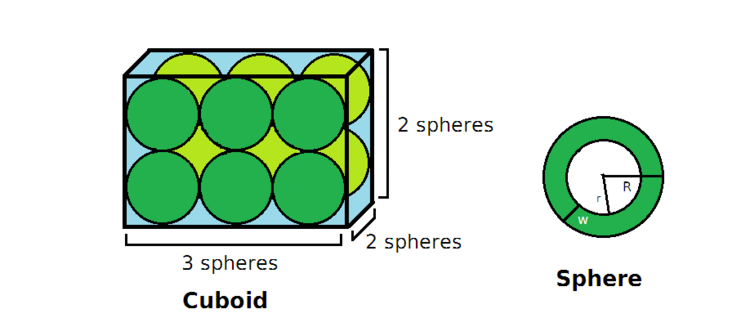 In a cuboid made of glass there are 12 spheres which perfectly fit in the cuboid in
orientation. All the spheres are identical. The dimensions of the cuboid
are in
ratio. The cuboid has an inner volume
, the sphere has an outer volume
, inner volume
, outer radius
, inner radius
and width
. The volume of the empty spaces in the cuboid
(i.e. difference between the volume of the cuboid and the volumes of all the spheres)
is equal to the inner volume of 30 such spheres. If the outer radius of a sphere is
, find
in terms of
.
In a cuboid made of glass there are 12 spheres which perfectly fit in the cuboid in
orientation. All the spheres are identical. The dimensions of the cuboid
are in
ratio. The cuboid has an inner volume
, the sphere has an outer volume
, inner volume
, outer radius
, inner radius
and width
. The volume of the empty spaces in the cuboid
(i.e. difference between the volume of the cuboid and the volumes of all the spheres)
is equal to the inner volume of 30 such spheres. If the outer radius of a sphere is
, find
in terms of
.
If for positive integers , we have , where , with minimized. Find the value of
The answer is 27.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Outer Radius of spheres ( R ) = x
Outer Diameter of spheres ( D = 2 × R ) = 2 x
Dimensions of cuboid ( l , b , h ) = 6 x , 4 x , 4 x
Volume of cuboid ( V c ) = 6 x × 4 x × 4 x = 9 6 x 3
Volume of 12 spheres ( 1 2 × V s ) = 1 2 × 3 4 π x 3 = 1 6 π x 3
Empty spaces in cuboid ( V c − 1 2 V s ) = 9 6 x 3 − 1 6 π x 3
= 1 6 x 3 ( 6 − π )
Inner raduis of sphere = r
Inner volume of 1 sphere ( v s ) = 3 4 π r 3
Inner volume of 30 spheres ( 3 0 × v s ) = 3 0 × 3 4 π r 3
= 4 0 π r 3
Empty spaces in cuboid ( V c − 1 2 V s ) = Inner volume of 30 spheres ( 3 0 × v s )
⟹ 1 6 x 3 ( 6 − π ) = 4 0 π r 3
⟹ 4 0 × π 1 6 x 3 × ( 6 − π ) = r 3
= 4 0 1 6 x 3 × π 6 − π = r 3
= 5 2 x 3 × ( π 6 − 1 ) = r 3
= x 3 × ( 5 2 ) ( π 6 − 1 )
= r 3 = x 3 × ( 5 π 1 2 − 5 2 )
⟹ r = x × 3 5 π 1 2 − 5 2
∴ a = 1 2 , b = 5 , c = 2 , d = 5 , e = 3 , a + b + c + d + e = 2 7