Not Three, But Four Incircles!
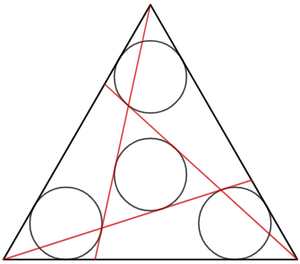
Four identical circles are positioned inside the unit equilateral triangle. Each of the three incircles is tangent to one of the three red lines, whereas the remaining incircle is positioned inside the central triangle.
If the radius of the circle is r , input ⌊ 1 0 5 r ⌋ as your answer.
The answer is 12276.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
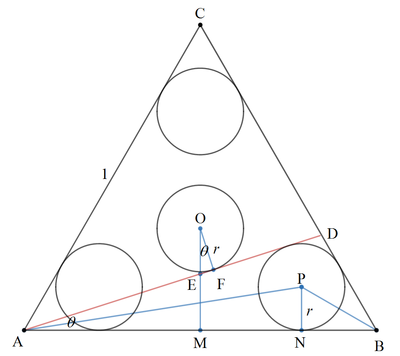
Label the unit equilateral triangle A B C , the bottom red line be A D , the centers of the central circle and the right circle be O and P respectively. Let O M and P N be perpendicular to A B , O M cuts A D at E , and the central circle tangent to A D at F .
Let ∠ D A B = ∠ E O F = θ . Then we have:
A N + N B r cot 2 θ + r cot 3 0 ∘ t r + 3 t ⟹ t = A B = 1 = 1 = t 1 + 3 1 = 3 t + 1 t Let t = tan 2 θ
Also
A M E M A M O M − O E 2 1 2 3 1 − r sec θ cos θ − 2 3 r ⟹ r = tan ∠ D A B = tan ∠ D A B = tan θ = 3 sin θ = 2 3 cos θ − 3 sin θ = 2 3 ( 1 + t 2 ) 1 − t 2 − 2 3 t
Therefore we have:
2 3 ( 1 + t 2 ) 1 − t 2 − 2 3 t ( 1 − 2 3 t − t 2 ) ( 1 + 3 t ) 3 3 t 3 + 7 t 2 + 3 3 t − 1 ⟹ t ⟹ r = 3 t + 1 t = 2 3 t ( 1 + t 2 ) = 0 ≈ 0 . 1 5 5 9 1 2 5 4 5 = 3 t + 1 t ≈ 0 . 1 2 2 7 6 1 1
Therefore ⌊ 1 0 5 r ⌋ = 1 2 2 7 6 .
Label the diagram as follows, and let A F = E D = k :
By the law of cosines on △ A D E , A D = D E 2 + A E 2 − 2 ⋅ D E ⋅ A E ⋅ cos ∠ D E A = k 2 + 1 − 2 ⋅ k ⋅ 2 1 = k 2 − 2 k + 1 .
Since △ A B F ∼ △ A E D by AA similarity, A B = A F ⋅ A D A E = k ⋅ k 2 − 2 k + 1 1 = k 2 − 2 k + 1 k and B F = A F ⋅ A D D E = k ⋅ k 2 − 2 k + 1 k = k 2 − 2 k + 1 k 2 = C D .
Then B C = A D − A B − C D = k 2 − 2 k + 1 − k 2 − 2 k + 1 k − k 2 − 2 k + 1 k 2 = k 2 − 2 k + 1 1 − 2 k .
As an incircle of the red equilateral, r = 2 3 1 ⋅ B C = 2 3 1 ⋅ k 2 − 2 k + 1 1 − 2 k = 2 3 k 2 − 2 k + 1 1 − 2 k .
As an incircle of △ A D E , r = D E + A E + A D D E ⋅ A E ⋅ sin ∠ D E A = k + 1 + k 2 − k + 1 k ⋅ 1 ⋅ 2 3 = 2 ( k + 1 + k 2 − 2 k + 1 ) 3 k .
So r = 2 3 k 2 − 2 k + 1 1 − 2 k = 2 ( k + 1 + k 2 − 2 k + 1 ) 3 k , which solves numerically to r ≈ 0 . 1 2 2 7 6 1 and k ≈ 0 . 3 1 1 5 4 9 .
Therefore, ⌊ 1 0 5 r ⌋ = 1 2 2 7 6 .