This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Or you could have taken the reflection of one point say ( 2 √ 2 , 2 √ 2 ) through the x − axis so that the minimum value would be the distance between ( √ 2 3 , √ 2 3 ) & ( 2 √ 2 , − 2 √ 2 ) .
It'd have been a fast move.
Chew-Seong Cheong, this is a stroke of genius! What a delight it was to read this solutions! Thanks for posting it.
Sir You are the most intelligent man on brilliant, hats off to you
Excellent solution. Thank you. I have solved using differential calculus concept.
Can't it be negative 5 because we have to find the minimum value of A ? And root can be negative.
Let's Do some geometric ! Let's The given expression in question be E
Now Inter-prate that This expression is written in form of cosine law .
According to figure :
 Figure
Figure
E = AD + DC
and By Triangle inequality in Triangle ADC :
A D + D C ≥ A C .
And For calculating AC note that Triangle ABC is right angled triangle.
So By Pythogoras Theoram :
A C = 5 .
E m i n = A m i n = 5 .
Q.E.D
whooaa !! Fab. Observation
I like your solution. Appreciable.
First Of all differentiate ′ A ′
d x d ( 1 9 + x 2 − 3 x 2 + 1 1 6 + x 2 − 4 x 2 ) = ( 2 x 2 − 4 x 2 + 1 6 2 x − 4 2 + 2 9 + x 2 − 3 x 2 2 x − 3 2 )
Now to maximize it
( 2 x 2 − 4 x 2 + 1 6 2 x − 4 2 + 2 9 + x 2 − 3 x 2 2 x − 3 2 ) = 0 ∴ x = 7 1 2 2
Now placing value of x in ′ A ′ we get A = 5
Its a challenge to all to solve ( 2 x 2 − 4 x 2 + 1 6 2 x − 4 2 + 2 9 + x 2 − 3 x 2 2 x − 3 2 ) = 0
Log in to reply
Actually its not that harder......it seems to be type of f'(x)/[f (x)]^n........
differentiate once,then equate to zero.....you'll get the value of "x",substitute in the equation and ....................job done :)
Would you please differentiate it STEP BY STEP
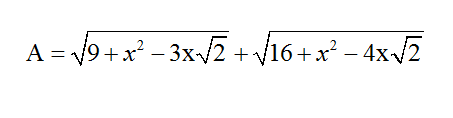
A = 9 + x 2 − 3 x 2 + 1 6 + x 2 − 4 x 2
= x 2 − 2 6 x + 2 9 + 2 9 + x 2 − 4 x 2 + 8 + 8
= ( x − 2 3 ) 2 + 2 9 + ( x − 2 2 ) 2 + 8
= ( x − 2 3 ) 2 + ( 0 − 2 3 ) 2 + ( x − 2 2 ) 2 + ( 0 − 2 2 ) 2
Therefore, A is the sum of lengths of two straight lines ( x , 0 ) , ( 2 3 , 2 3 ) and ( x , 0 ) , ( 2 2 , 2 2 ) .
The shortest total length is that traveled by light from ( 2 3 , 2 3 ) to ( 2 2 , 2 2 ) reflected at the x -axis at ( x , 0 ) . And the angle of incident = angle of reflection.
Therefore, 2 3 x − 2 3 = 2 2 2 2 − x ⇒ 3 2 x − 1 = 1 − 2 2 1 x
⇒ ( 3 2 + 2 2 1 ) x = 2 ⇒ ( 3 2 + 4 2 ) x = 2 ⇒ 1 2 7 2 x = 2 ⇒ x = 7 1 2 2
Substitute x = 7 1 2 2 in A , we have:
A m i n = ( 7 1 2 2 − 2 3 2 ) 2 + 2 9 + ( 7 1 2 2 − 2 2 ) 2 + 8
= ( 1 4 3 2 ) 2 + 2 9 + ( − 7 2 2 ) 2 + 8
= 1 9 6 1 8 + 2 9 + 4 9 8 + 8 = 1 9 6 9 0 0 + 4 9 4 0 0 = 5