Not your average shuriken
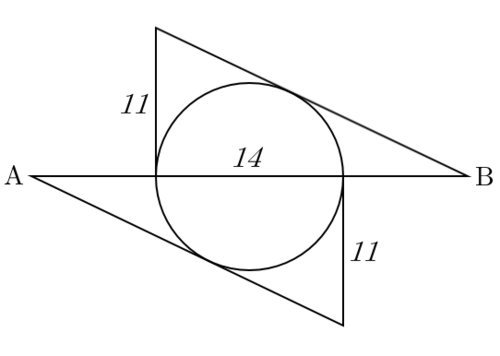 A circle of diameter
1
4
has two identical right triangles that are circumscribed around the two semicircles created by the line
A
B
cutting the circle in half.
A circle of diameter
1
4
has two identical right triangles that are circumscribed around the two semicircles created by the line
A
B
cutting the circle in half.
If the short legs of the right triangles are 1 1 as shown, the length of A B can be written as b a , where a and b are co-prime integers. Find a b .
Try another geometry problem: "Star Stumper" .
The answer is 10710.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
Moderator note:
Splendid as always!
Wow. Splendid!
The Sage strikes again! :)
Guys!! that two lines are || . Be simple. simply you will get answer.
Just for sake of variety ....
Let O be the center of the circle and T be the point of tangency of the "top" right triangle with the circle. Also, let the lower-left vertex of this triangle be Q and its uppermost vertex be P .
Then Δ P Q B and Δ O T B are similar triangles. Now let ∣ O B ∣ = x and ∣ T B ∣ = y . Since ∣ P T ∣ = ∣ P Q ∣ = 1 1 and ∣ Q O ∣ = 7 , we have by similarity that
∣ Q B ∣ ∣ P Q ∣ = ∣ T B ∣ ∣ O T ∣ ⟹ 7 + x 1 1 = y 7 ⟹ 1 1 y − 7 x = 4 9 . (i),
and also that
∣ P B ∣ ∣ P Q ∣ = ∣ O B ∣ ∣ O T ∣ ⟹ 1 1 + y 1 1 = x 7 ⟹ 1 1 x − 7 y = 7 7 , (ii).
Multiplying (i) by 7 and (ii) by 1 1 and adding the resulting equations gives us that
− 4 9 x + 1 2 1 x = 7 ∗ 4 9 + 1 1 ∗ 7 7 ⟹ x = 7 2 1 1 9 0 = 3 6 5 9 5 .
Now ∣ A B ∣ = 2 x = 1 8 5 9 5 , so a b = 5 9 5 ∗ 1 8 = 1 0 7 1 0 .
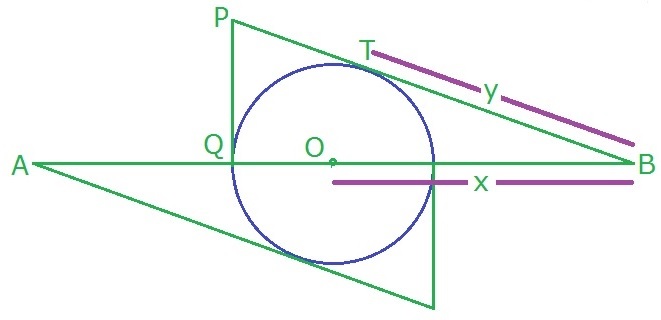
Let point C , D be the intersections of line A B through the circle from left to right. Let point E be the other vertex of the right triangle on the top semicircle as shown. B E is the tangent line that intersects with the circle at point F .
Since both E C and E F are tangents to the circle, E C = E F = 1 1 . Let B D = x and B F = y , by the power of the point theorem, we have
y 2 = x ( x + 1 4 ) ⟹ y 2 − x 2 = 1 4 x . (1)
According the Pythagorean Theorem, 1 1 2 + ( x + 1 4 ) 2 = ( y + 1 1 ) 2 .
Regroup the equation and substitute (1) we have 1 2 1 + 2 2 y = 1 4 x + 3 1 7 .
Therefore, y = 1 1 7 ( x + 1 4 ) . (2)
Substitute (2) into (1),
1 2 1 ( x 2 + 1 4 x ) = 4 9 ( x 2 + 2 8 x + 1 9 6 ) , ⟹ x = 3 6 3 4 3 .
Thus, A B = 2 × 3 6 3 4 3 + 1 4 = 1 8 5 9 5 = b a .
We have a b = 5 9 5 × 1 8 = 1 0 7 1 0 .
ah.. I too got it with a same approach
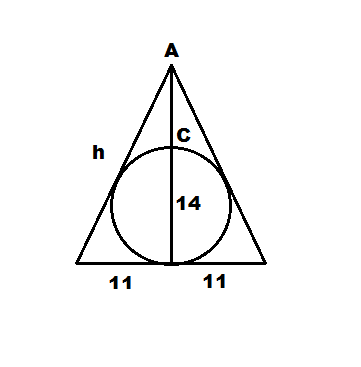
Since the triangles are similar you can look at the figure like this.
AB = 14 + 2AC. We can use the formula r = Area of triangle (A)/semi-perimeter of triangle (s). Since you're given the radius (7) and the base (22), you can get the value of h. h = 935/36.
Using Pythagorean theorem. You can get the value of the other leg. The value of the other leg is 847/36.
AC = 847/36 - 14
AC = 343/36
AB = 14 + 2(343/36)
AB = 595/18
ab = 595*18 = 10710
A
B
=
2
∗
(
L
o
n
g
l
e
g
)
−
D
i
a
m
e
t
e
r
=
2
∗
1
1
∗
T
a
n
{
2
∗
T
a
n
−
1
(
7
/
1
1
)
}
−
1
4
=
2
2
∗
1
−
(
1
1
7
)
2
2
∗
1
1
7
−
1
4
=
1
8
8
4
7
−
1
4
=
1
8
5
9
5
=
b
a
.
∴
a
∗
b
=
1
0
7
1
0
.
Firstly, B D = y and B G = x
Since C E and D E are tangents, C E = E D = 1 1
C F = F G = 2 1 4 = 7 since B D is a tangent.
Now applying Pythagorean Theorem to the right triangles F D B and E C B , we have the following pair of equations:
7 2 + y 2 = ( 7 + x ) 2 and 1 1 2 + ( 1 4 + x ) 2 = ( 1 1 + y ) 2
Solving for x , we come across a quadratic equation 3 6 x 2 + 1 6 1 x − 4 8 0 2 = 0 . The only legitimate value of x happens to be 3 6 3 4 3 .
Now, we have A B = 1 4 + 2 x = 1 8 5 9 5
Multiplying their numerator and denominator, we have 5 9 5 × 1 8 = 1 0 7 1 0
Connect center of circle O to a point C on the point of tangency of the upper right triangle.
Connect these to points to get O C , the radius, which is 7 .
This forms 2 right triangles that are similar by A A .
Call C B = x
We set up a proportion: h y p h y p = l e g l e g
The hypotenuse of the smaller right triangle is x 2 + 7 2
Substitute the known values into the proportion: 1 1 + x x 2 + 7 2 = 1 1 7
Solve this equation to get x = 3 6 5 3 9
Thus A B = 2 ( ( 3 6 5 3 9 ) 2 + 7 2 − 7 ) + 1 4 (from the Pythagorean theorem for the smaller triangle)
A B = 1 8 5 9 5
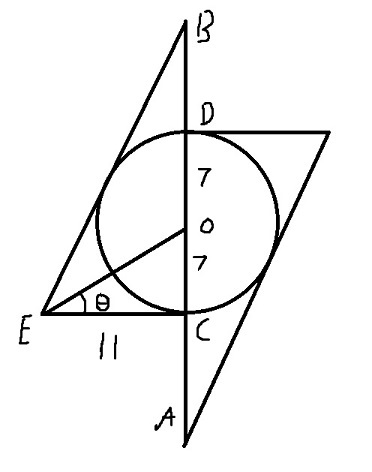
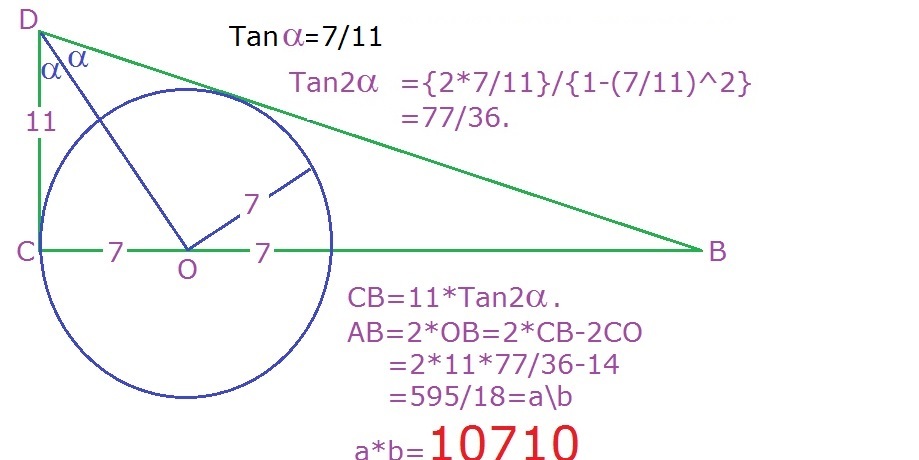
Firstly, notice that C E and B E are both tangents to the circle. This means that angles ∠ B E O and ∠ O E C are the same. tan ( ∠ O E C ) = 7 / 1 1 so t a n ( ∠ B E C ) = tan ( 2 ∠ O E C ) = 1 − ( 1 1 7 ) 2 2 1 1 7 = 3 6 7 7
From tan ( ∠ B E C ) = 1 1 C B , C B = 1 1 . 3 6 7 7 = 3 6 8 4 7 As the diagram is symmetrical and D B = C B − C D = 3 6 8 4 7 − 1 4 = 3 6 3 4 3 A B = A C + C D + D B = 3 6 3 4 3 + 1 4 + 3 6 3 4 3 = 1 8 5 9 5
Multiplying out gives the answer.

A B = 2 x = cos ( 2 θ ) 1 4 = 1 − 2 sin 2 θ 1 4 = 1 − 1 1 2 + 7 2 2 × 7 2 1 4 = 1 8 5 9 5