Not your typical car problem
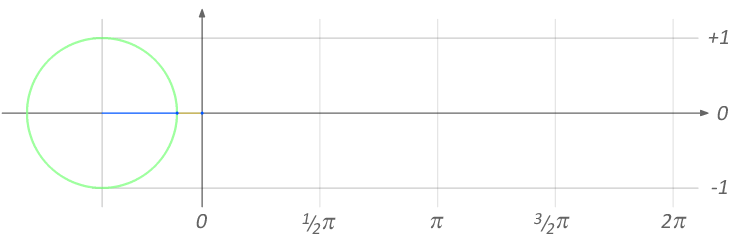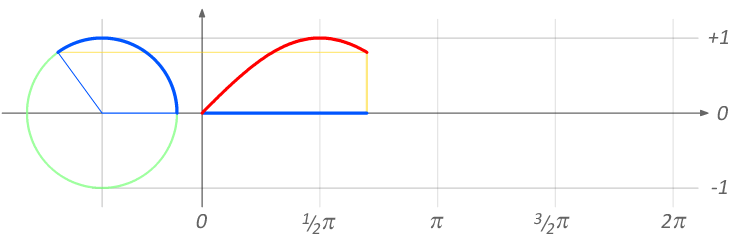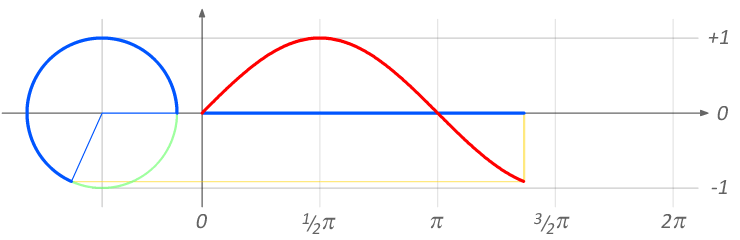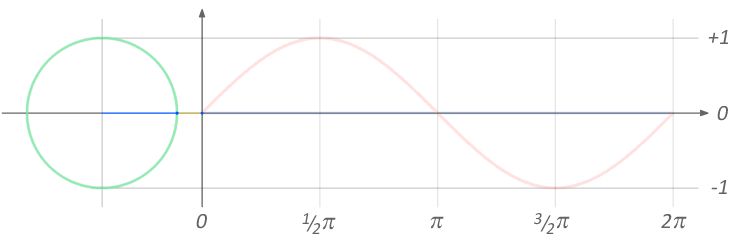 A certain road follows the path of a sine wave, with the equation
, whose origin represents the starting point of the road. If a car is travelling at this road starting at its origin, at an instantaneous speed of
m/s, as the car moves farther, determine the limiting rate (in m/s) as to how the car separates from the origin.
A certain road follows the path of a sine wave, with the equation
, whose origin represents the starting point of the road. If a car is travelling at this road starting at its origin, at an instantaneous speed of
m/s, as the car moves farther, determine the limiting rate (in m/s) as to how the car separates from the origin.
Note:
The values of and are in meters.
Clarification: In the graph above, the car follows the red path.
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The instantaneous distance of the car from the origin (shown in violet), can be represented by y = ( x 2 + s i n 2 ( 6 π x ) ) .
By virtue of related rates, we see that
d t d y = d x d y ⋅ d t d x
However, instead of d t d x , we are given with the rate of the car along the graph of y = s i n ( 6 π x ) . If we let this given rate as d t d L , then we can derive a relationship that
d t d x = d L d x ⋅ d t d L , simplifying our original equation to
d t d y = d x d y ⋅ d L d x ⋅ d t d L
Now, we will have to find d L d x . Note that L = ∫ 1 + ( y ′ ) 2 d x
thus, d x d L = 1 + 3 6 π 2 c o s ( 6 π x ) .
It follows that
d L d x = 1 + 3 6 π 2 c o s ( 6 π x ) 1 .
Now, we have d L d x and d t d L . We can easily get the derivative d x d y and get
6 x 2 + sin 2 ( 6 π x ) 6 x + π sin ( 6 π x ) cos ( 6 π x ) .
So,
d t d y = d x d y ⋅ d L d x ⋅ d t d L and get 6 x 2 + sin 2 ( 6 π x ) 6 x + π sin ( 6 π x ) cos ( 6 π x ) ⋅ 1 + 3 6 p i 2 c o s ( 6 p i x ) 1 ⋅ 3 x 2 − 1 9 x 2 1 + 3 6 π 2 c o s 2 6 π x
Simplifying that, we get
d x d y = 6 x 2 + sin 2 ( 6 π x ) 6 x + π sin ( 6 π x ) cos ( 6 π x ) ⋅ 3 x 2 − 1 9 x 2 .
We are asked to find out lim x → ∞ ( d x d y ) .
And here, by use of squeeze theorem, L'Hopital's rule and other related theorems,
x → ∞ lim ⎝ ⎜ ⎜ ⎛ 6 x 2 + sin 2 ( 6 π x ) 6 x + π sin ( 6 π x ) cos ( 6 π x ) ⋅ 3 x 2 − 1 9 x 2 ⎠ ⎟ ⎟ ⎞ = 3