Not Your Usual Cone

A brief solution is as follows: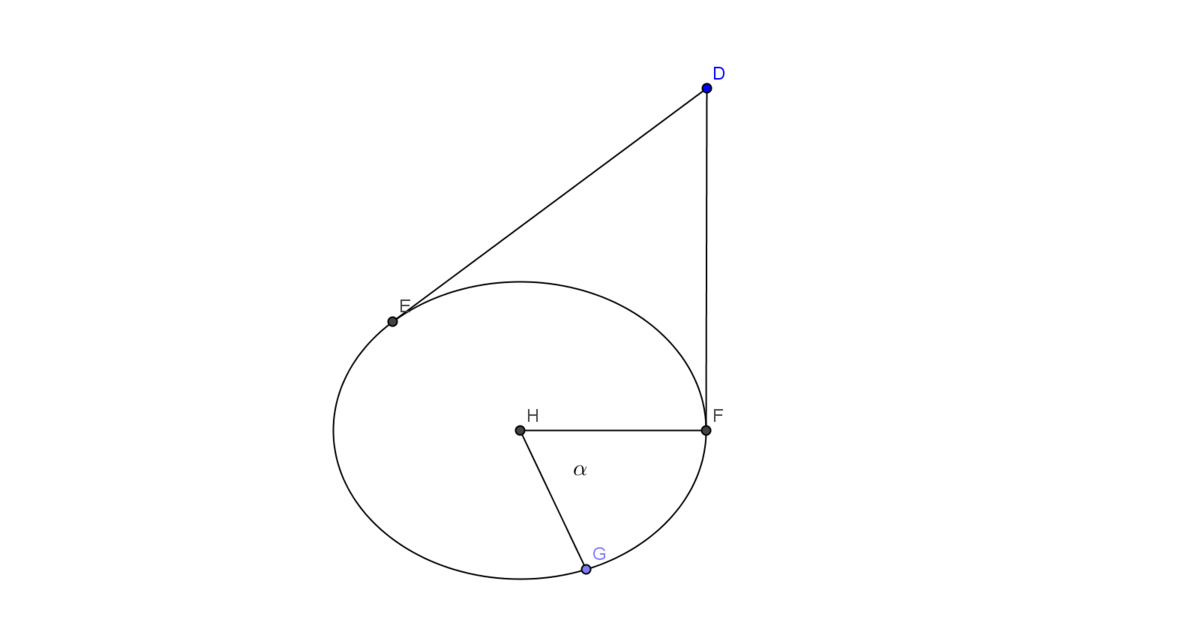

• Consider the base circle of radius $r$ and angle $\alpha$ as parametric angle of $G$ .

• We will calculate the curved angle by considering thin triangles having base of $rd\alpha$ .

• The height of this thin triangle (at $G$ ) is equal to the distance between the tangent at $G$ to the base, and the vertex $D$ , say $H(\alpha)$ as height is a function of $\alpha$ .

• By using vectors (or standard 3D geometry distance calculations), we can show that, $\quad \quad \quad \quad \quad \quad H(\alpha )\quad =\quad \sqrt { { (r+d(cos\alpha )) }^{ 2 }+{ h }^{ 2 } }$

Where $d$ is the distance through which the vertex has been shifted from the right circular case. $d = \sqrt{a^{2} - h^{2}}$

• As base is $r(d\alpha$ ) and height is $H(\alpha)$ the curved surface area of the cone equals

$\quad \quad \quad \quad \quad \quad C.S.A\quad =\quad 2\int _{ 0 }^{ \pi }{ \cfrac { 1 }{ 2 } (H(\alpha )) } r(d\alpha )$

(twice for the $\pi$ to 2 $\pi$ part)

• This integral can be evaluated to $49.947$ .

• This is added to the base area to get total surface area $\boxed{78.221}$