Not Your Usual Cylinder - Volume
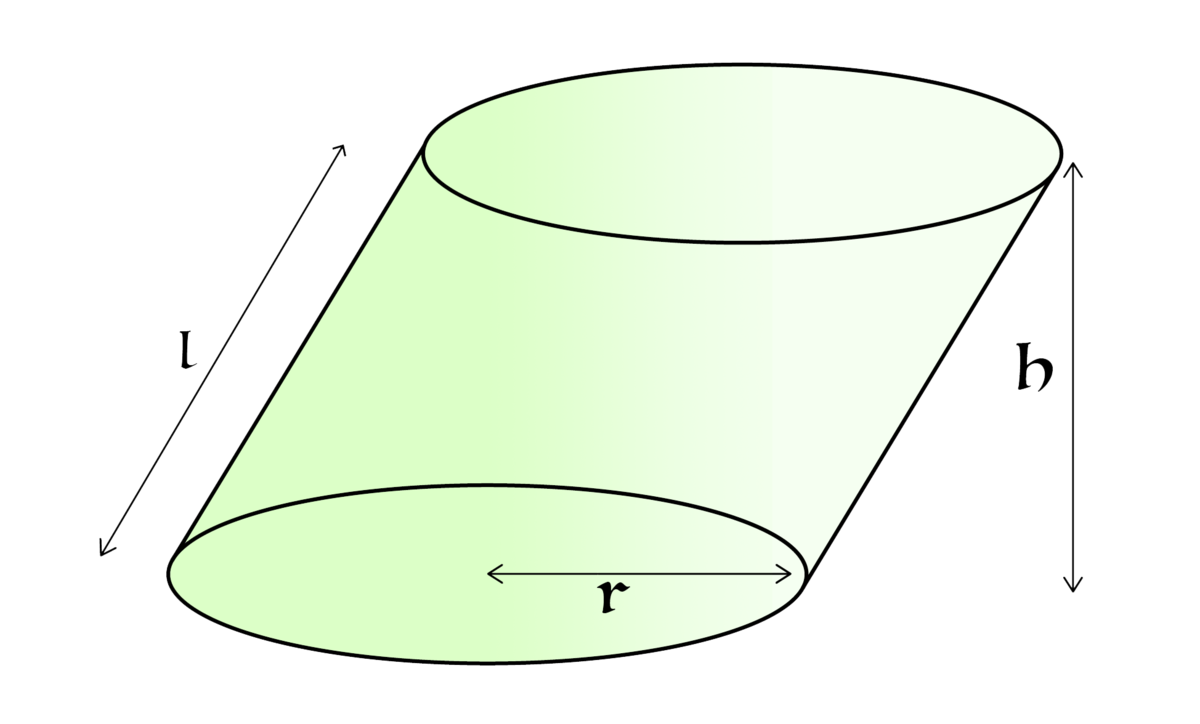
Given the following information, find the volume of the oblique cylinder shown above:
- The flat sides of the cylinder are circular, congruent and parallel to each other.
- The slant height of the cylinder is
- The radius of the circular base is
- The perpendicular height of the cylinder is
- The image is not drawn to scale.
State your answer to five significant figures.
Also try: Not Your Usual Cylinder - Surface Area
The answer is 50.265.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If you take a rectangle and displace one of its sides parallel to the other side the area of the shape does not change. All the parallelograms thus formed have the same base length, the same perpendicular height and therefore have the same area. This is a 2-dimensional example of Cavalieri's principle .
Similarly, if you take a right cylinder and displace one of its flat faces parallel to the other flat face, then you obtain an oblique cylinder with the same volume as the original right cylinder. This is a 3-dimensional example of Cavalieri's principle .
The right cylinder will have the same perpendicular height as the oblique cylinder, h = 4 . The radius of the circular base will be r = 2 . Therefore the volume of the right cylinder, and also the volume of the oblique cylinder is π × r 2 × h = π × 2 2 × 4 = 1 6 π ≈ 5 0 . 2 6 5 □
You can also check out this interactive Math Open Reference link where you can adjust the height, radius, and the slant height of the cylinder and observe how the volume changes. (Click 'options' in lower right corner to 'allow oblique' and 'freeze height'.)