Now I Know My ABCs

Let $x=b^c$ , then we have:

$\begin{aligned} a^{b^c} & = b^c \\ a^x & = x \\ x \ln a & = \ln x \\ \frac{d}{dx} x \ln a & = \frac{d}{dx} \ln x \\ \ln a + \frac{x}{a} \dot{} \frac{da}{dx} & = \frac{1}{x} \\ \frac{da}{dx} & = \frac{a(1-x\ln a)}{x^2} \\ & = \frac{a(1-\ln x)}{x^2} \end{aligned}$

$\begin{aligned} \text{Equating } \frac{da}{dx} & = 0 \\ \Rightarrow 1-\ln x & = 0 \\ \ln x & = 1 \\ x & = e \end{aligned}$

When $x = e, \quad \Rightarrow e\ln a = \ln e \quad \Rightarrow \ln a = \frac{1}{e} \quad \Rightarrow a = e^{\frac{1}{e}}$ and

$\begin{aligned} \frac{d^2a}{dx^2} & = \frac{1-\ln x}{x^2}\dot{} \frac{da}{dx} - \frac{2ax ( 1-\ln x)}{x^3} - \frac{a}{x^3} \\ & = 0 - 0 - e^{\frac{1}{e}-3} < 0 \end{aligned}$

$\Rightarrow a_{max} = \boxed{e^{\frac{1}{e}}}$

Let $b^{c}=x$ . We know that $x>0$ because a positive real number raised to a positive real number is a positive real number.

We also know that all possible values for $x$ are possible values for $b^{c}$ by letting $b=x$ and $c=1$ .

Now, we are left with the equation $a^{x}=x$ . By raising both sides to the $\frac{1}{x}$ power we end up with $a=x^{\frac{1}{x}}$ .

Next, we want to use the fact that $k=e^{ln(k)}$ for $k>0$ in order to take the derivative of our equation.

We end up with $a=e^{ln(x^{\frac{1}{x}})}$ which, by using logarithm rules can be rewritten once again as $a=e^{\frac{1}{x}ln(x)}$ .

This is now in a form that we can easily differentiate.

$\frac{da}{dx}=e^{\frac{1}{x}ln(x)}(\frac{1}{x} \times \frac{1}{x}+\frac{-1}{x^{2}} \times ln(x))$

Now, we need to find out where $\frac{da}{dx}=0$ in order to find critical points.

In our derivative, we essentially have two functions of $x$ multiplied together. So, if one of those equals $0$ then $\frac{da}{dx}=0$ . Our first is $e^{\frac{1}{x}ln(x)}$ which can't equal $0$ over all real numbers, so it certainly can't equal zero over the positive real numbers. our second is $\frac{1}{x^{2}}+\frac{-1}{x^{2}}ln(x)$ , which can be rewritten as $(\frac{1}{x^{2}})(1-ln(x))$ .

$\frac{1}{x^{2}}$ cannot equal $0$ over all real numbers, so again it cannot equal $0$ over positive real numbers. The second piece $1-ln(x)$ CAN equal 0 however, at $ln(x)=1$ , or $x=e$

Here, it is very important to note that $e^{\frac{1}{x}ln(x)}$ and $\frac{1}{x^{2}}$ will both always be positive over the real numbers, so the sign of our derivative, now expressed as $\frac{da}{dx}=e^{\frac{1}{x}ln(x)}(\frac{1}{x^{2}})(1-ln(x))$ will be determined entirely by the sign of $1-ln(x)$ . Since $ln(x)$ is an increasing function, $1-ln(x)$ will change sign from $+$ to $-$ at $x=e$ .

So, by the first derivative test, since $\frac{da}{dx}=0$ at $x=e$ and $\frac{da}{dx}$ changes sign from $+$ to $-$ at $x=e$ , $x=e$ is a maximum value of $a$ .

FINALLY, since we know that our maximum for $a$ is at $x=e$ , and that $a=x^{\frac{1}{x}}$ , the maximum value of $a$ is $\boxed{e^{\frac{1}{e}}}$

We can write $b^c$ as $x > 0$ , so our equation is $a^x = x$ . That means $x\ln a = \ln x$ , for a given $x$ .

Knowing the graph of $y=\ln x$ , we want to find its intersection with the line $y=x \ln a$ .

The slope of the line increases as $a$ is increased. As we can see in the picture below, the line meets $y = \ln x$ twice for small values of $a$ , and we can keep increasing $a$ until the line becomes tangent to the curve, when the maximum value $a_{\small MAX}$ is reached.

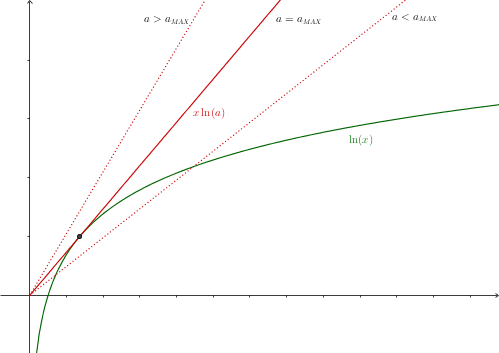
At the point of tangency, the slope of the curve is $y' = \dfrac1x$ . The slope of the line is $\ln a$ , but since $x\ln a = \ln x$ , then $\ln a = \dfrac{\ln x}x$ ( $x$ being the horizontal coordinate of the point of tangency).

As we know, the slope of the curve at the point of tangency is equal to the slope of the line. Then, $\dfrac1x = \dfrac{\ln x}x\\\ \\1 = \ln x\\x = e\$ That means $\ln a = \dfrac{\ln x}x = \dfrac{\ln e}e = \dfrac1e$ , giving $a = e^{\frac1e}$ .