Now it gets hard

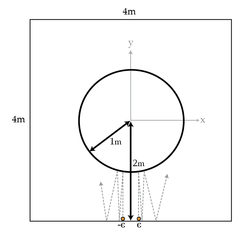So far we've understood that chaos stems from nearby paths diverging over time. A circle in the middle of the table will always cause nearby paths to diverge and hence that is the shape that makes the system chaotic.

Let's do some quantitative analysis of the table with a circle. The circle in the middle is given by the equation $x^2+y^2=1$ . You start two (infinitesimally small) billiard balls at $x=\pm \epsilon,y=-2$ with a velocity purely in the positive y-direction. $\epsilon$ can be taken to be very small. What is the ratio of the distance apart the disks are after the 25th time they bounce off the side of the table to their distance after the 5th time they bounce off the side of the table? You may assume $N>>1$ , but $N\epsilon<<1$ m.