Now it gets hard
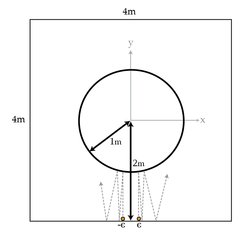 So far we've seen that chaos stems from nearby paths diverging over time. A circle in the middle of a table will always cause nearby paths to diverge and hence will makes the system chaotic.
So far we've seen that chaos stems from nearby paths diverging over time. A circle in the middle of a table will always cause nearby paths to diverge and hence will makes the system chaotic.
The circle in the middle is given by the equation x 2 + y 2 = 1 . You start two (infinitesimally small) billiard balls at x = ± ϵ , y = − 2 with a velocity purely in the positive y-direction. ϵ can be taken to be very small.
What is the ratio of the distance apart the disks are after the 25th time they bounce off the side of the table to their distance after the 5th time they bounce off the side of the table? You may assume N ≫ 1 , but N ϵ ≪ 1 m.
This problem is part of David's Complete And Utter Chaos set.
The answer is 2.05E+15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Do we assume that it will always hit the circle? not hitting the other sides of the table?
I thought I understood your solution at first, Could you please explain why ϕ = x n + θ
Log in to reply
If Q is the point where collision between circle and particle is taking place, ϕ ≈ C P P Q ≈ A Q θ n + x n ≈ x n + θ n ,as A Q ≈ O P = 1
Nice solution! Brilliant!..
How you solved the final equation in box to get the value to Xn in terms of € and n...?
Did it the same way !!!!!
I formed a recurrence relation here and solved. In the diagram, the angles have been larger than they really are .
Clearly, the angle of incidence is same as angle of reflection, as the magnitude of components along common tangent and normal of ball and circle remain same.
Refer to the diagram. Here, the trajectory of particle between n th and n + 1 th bounce is shown.
Now, say atr N bounce from side of table , the distance from O is x n , i.e. O A = x n . Then, O B = x n + 1 . Clearly, x 0 = ϵ .
Also, say θ n is the angle that the motion of ball makes with vertical(the line that seems vertical in the diagram). Clearly θ 0 = 0
Using O P = 1 , C P = 1 , we have
ϕ = x n + θ n
θ n + 1 = 2 ϕ + θ = 2 x n + 3 θ n ...... (i)
x n + 1 = x n + θ + 2 ϕ + θ
⇒ x n + 1 = 3 x n + 4 θ n .... (ii)
From (ii),
θ n = 4 1 ( x n + 1 − 3 x n )
Putting this in in (i),
θ n + 1 = 2 x n + 4 3 ( x n + 1 − 3 x n )
Thus, θ n = 2 x n − 1 + 4 3 ( x n − 3 x n − 1 )
Putting this value in (ii),we have
x n + 1 = 6 x n − x n − 1 ,
where x 0 = ϵ , x 1 = 3 ϵ
Hence, we can have x n = 2 ϵ ( ( 3 + 2 2 ) n + ( 3 − 2 2 ) n ) , and x 5 x 2 5 ≈ 2 . 0 5 E + 1 5