Now we're introducing "Limits" in Geometry!
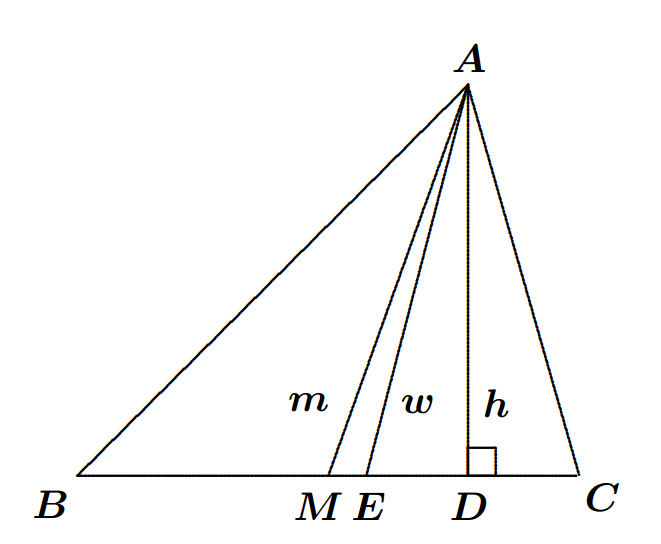 Let
and
be the lengths of the median, the angle bisector and the altitude, respectively, from the right-angled vertex
of a triangle
to the hypotenuse. Suppose that the side
is fixed in length, while the side
varies subject to
. Evaluate the value of the following correct upto three places of decimals:
Let
and
be the lengths of the median, the angle bisector and the altitude, respectively, from the right-angled vertex
of a triangle
to the hypotenuse. Suppose that the side
is fixed in length, while the side
varies subject to
. Evaluate the value of the following correct upto three places of decimals:
The answer is 4.000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Without loss of generality, we may assume that the side length c = 1 . Let us embed the triangle A B C into the Euclidean plane R 2 as follows. Place it so that the vertex A is at the origin, the vertex B at the point ( 0 , 1 ) , and the point C as a variable point ( c , 0 ) . We then have explicit formulae for w , m , h as functions of c . In particular, we realize that m ( c ) is simply half the length of the hypotenuse, whence m ( c ) = 2 1 + c 2 . Next, let W be the point of intersection of the hypotenuse and the line y = x . Then w ( c ) is the length of the line segment A W . The hypotenuse lies on the line with equation y = c − x + 1 , whence W has coordinates ( c + 1 c , c + 1 c ) . Thus w ( c ) = c + 1 2 c . Finally, we may compute h ( c ) via similar triangles and deduce that 1 h ( c ) = 1 + c 2 c . Thus the desired limit is equal to c → 1 lim c + 1 2 c − c 2 + 1 c 2 1 + c 2 − 1 + c 2 c = c → 1 lim 2 c ( 2 c 2 + 2 − c − 1 ) ( c − 1 ) 2 ( c + 1 ) . We can evaluate this limit by the usual conjugation trick in first year calculus, to obtain the limit c → 1 lim 2 c ( 2 c 2 + 2 − c 2 − 2 c − 1 ) ( c − 1 ) 2 ( c + 1 ) ( 2 c 2 + 2 + c + 1 ) = c → 1 lim 2 c ( c + 1 ) ( 2 c 2 + 2 + c + 1 ) = 4 , by inspection.