NSEJS #3
Electricity and Magnetism
Level
3
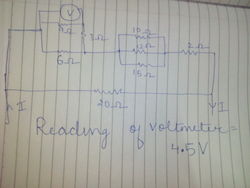 Assume that the voltmeter is ideal, find current through
resistor
Assume that the voltmeter is ideal, find current through
resistor
This is the part of this set .
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The potential drop across the 9 o h m resistor is 4 . 5 V . So, by Ohm's law, current through it (from left to right):
i = 9 4 . 5 = 0 . 5 A This is the same current that flows through the 3 o h m resistor hence the same current flows through their series combination of 9 + 3 = 1 2 o h m s . Let's establish that current I when comes across two resistors of 1 2 o h m s and 6 o h m s divides such that the 1 2 o h m s resistor receives a current of 0 . 5 A .
Now, if the equivalent resistance of the 1 0 o h m s and 1 5 o h m s resistors is calculated it comes out to be:
R e q 1 = 1 0 1 + 1 5 1 = > R e q = 6 o h m s
This again creates the situation in which current I has to divide between resistors of resistances 6 o h m s and 1 2 o h m s . Therefore, the current through the 1 2 o h m s resistor is 0 . 5 A .