Remainder Challenge
Find the remainder when 6 9 8 + 8 9 8 is divided by 98.
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
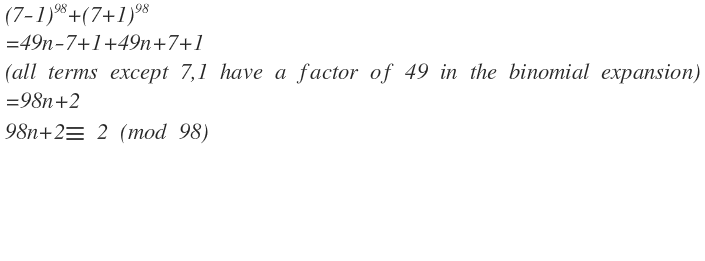
Can you explain how did you get (7-1)^98 as 49n -7+1 ?
Log in to reply
I used the binomial expansion of (7 -1)^98 and (7+1)^98. You will notice that all odd powers of 7 cancel. All terms except the last 2 have a power of 7 greater than 2 ie they are divisible by 49.
I thought of this same method!
Isn't true 8^98-6^98> (49n+7+1-(49n-7+1))=14 (7+1)^98+(7-1)^98=49 n-7 98+1+49 m-7 98+1= 49(n+m)+2 6^98+8^98=0 (mod 2) 6^98+8^98=2 (mod 49) So 6^98+8^98=49k+2 k=2p so 6^98+8^98=98p+2 So answer is 2
If f(x)=6^x+8^x is divisible by x then x=0 should yield no remainder so answer is 6^0+8^0=2
By Fermat's Little Theorem,
6^97 is congruent to 1 mod 98.
8^ 97 is congruent to 1 mod 98.
1 + 1 = 2.. And we're done.
The question was about 6^98+8^98 not 6^97+8^97, in any case 6^97=90(mod98), and 8^97=92(mod98) not 1 and 1. And for clarity 6^98=50(mod98) and 8^98=50(mod98). Fermat's lil' thm doesn't apply, but Euler's theorem using totients does, though I don't think either is necessary for this problem, but could be used to shorten some work.
Log in to reply
Ya you are correct
Even Euler's theorem wont work as 6 and 98 are not coprime. A more general case of Fermat's Little theorem which is a^p = a mod p where a is any number might have worked but in this case 98 is not a prime. So the way is either binomial theorem or Chinese Remainder theorem(or even by division algorithm) by breaking 98 into 2 and 49 which are coprime and then solving
98 and 6 are not co-prime, which is the prerequisite to apply fermat' theorem
And yet..........
Yeah fermat's little theorem can't b used........ U can't manipuplate things
ficjnvqpcvja;
We can do it by fermats little theorem as 6^98=remainder 36 on dividing by 98 and 8^98=64 remainder on dividing by 98. Thus 64+36=100 divided by 98 leaves remainder 2. So remainder is 2
Hey, this is absolutely wrong! Fermat's little theorem tells us that a^p-1 = 1(mod p), where p is a prime and ("=" means congruent) and gcd(a, p) = 1. You have used Fermat's L. Theorem for 98 which is not prime and hence solution is completely wrong!
Now, I know that the staff will say : "" Oh, but 98 is not prime. So you cannot use Fermat's Little Theorem"".
Well, let's be practical. In these types of problems, the modulus does not need to be prime. Trust me.
Log in to reply
Sir the question is never about practicality but whether it is the correct method. If you can prove that in these problems we the number need not be prime, then Ill agree with you
6 9 8 + 8 9 8 = ( 7 − 1 ) 9 8 + ( 7 + 1 ) 9 8
By The Binomial Expansion Theorem ,
( 7 − 1 ) 9 8 = 7 9 8 ( − 1 ) 0 + 9 8 ⋅ 7 9 7 ( − 1 ) 1 . . . + 9 8 ⋅ 7 1 ( − 1 ) 9 7 + 7 0 ( − 1 ) 9 8
( 7 + 1 ) 9 8 = 7 9 8 1 0 + 9 8 ⋅ 7 9 7 1 1 . . . + 9 8 ⋅ 7 1 1 9 7 + 7 0 1 9 8
Since all of the terms except for the last 2 in each expansion contain 7 to a power of at least 2,
( 7 − 1 ) 9 8 + ( 7 + 1 ) 9 8 ≡ 0 ( m o d 4 9 ) + ( 9 8 ⋅ 7 1 ( − 1 ) 9 7 + 7 0 ( − 1 ) 9 8 ) ( m o d 4 9 ) + 0 ( m o d 4 9 ) + ( 9 8 ⋅ 7 1 1 9 7 + 7 0 1 9 8 ) ( m o d 4 9 )
≡ ( 9 8 ⋅ 7 ⋅ − 1 + 1 + 9 8 ⋅ 7 ⋅ 1 + 1 ) ( m o d 4 9 )
≡ 2 ( m o d 4 9 )
That means
6 9 8 + 8 9 8 ≡ 2 ( m o d 9 8 ) OR
6 9 8 + 8 9 8 ≡ 5 1 ( m o d 9 8 )
Since 6 9 8 + 8 9 8 is even,
6 9 8 + 8 9 8 ≡ 2 ( m o d 9 8 )
We have 6^98+8^98 ≡ 2 (mod 49) and 6^98 + 8^98 ≡ 0 mod 2 . Using Chinese Remainder Theorem(which would work as 2 and 49 are co prime) or Euclid's division algorithm. We have 6^(98)+8^(98) = 98k + 2 where k is a fixed integer which need not be calculated in the context of the problem . So The remainder is 2