This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Discussions for this problem are now closed
One prove is the 2's multiplication. First you have 2.
2 × 2 = 4
2 × 2 × 2 = 8
2 × 2 × 2 × 2 = 1 6
In the 16 the 6 when multiplied by 2 results in 12. You have 2 again. This 2 makes a 4, the 4 makes a 8 and the 8 makes a 16. The 16 makes 32, because the 6 becomes 12.
Simple . If you multiply 256 with 2 , obvious its going to be 2 at the end.
Moderator note:
That's one way of seeing it. But how would you find the last digit of something far much larger, say 2 1 2 3 4 5 6 ?
we can observe the last digit it is repeating as 2,4,8,6
Moderator note:
Your solution is incomplete. You did not explain why the digits repeats? Why would the last digits of 2 1 0 0 1 , 2 1 0 0 2 , 2 1 0 0 3 , 2 1 0 0 4 be 2 , 4 , 8 , 6 as well instead of something else?
it 2 multiplying itself 9 times which gives us 512 hence 2 the last digit of the product value
The pattern is highlighted in red. The pattern is 2 4 8 6. And if you still do not trust that, then just use a calculator. But either way, the answer is 2.
Moderator note:
We often try to avoid using tables or calculators if one isn't needed.
That's perfect
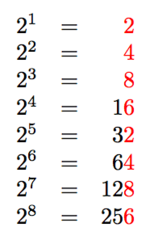
The last digit is 2.
If you observe the pattern of red digits, you see that it repeats in the form 2, 4, 8, 6. Hence, the next value is 2. (How would you prove that this pattern exists?)
Also, if you know that 2 9 = 5 1 2 , then the last digit is 2.