Number Theory
Number Theory
Level
3
Find the sum of all positive two-digit integers that are divisible by each of their digits.
Source: AIME 2001.
The answer is 630.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Assume that the number is AB.
It can be written as (10×A)+B
According to the question, both A & B must divide (10×A)+B
Then we can conclude, [(10×A)+B] is divisible by A if B is divisible by A & [(10×A)+B] is divisible by B if 10×A is divisible by B.
The above two conditions must be satisfied simultaneously.
Mathematically,
B = KA [where K is a constant]
10A = LB [where L is a constant]
Now, all possibilities for first condition in tabulated form: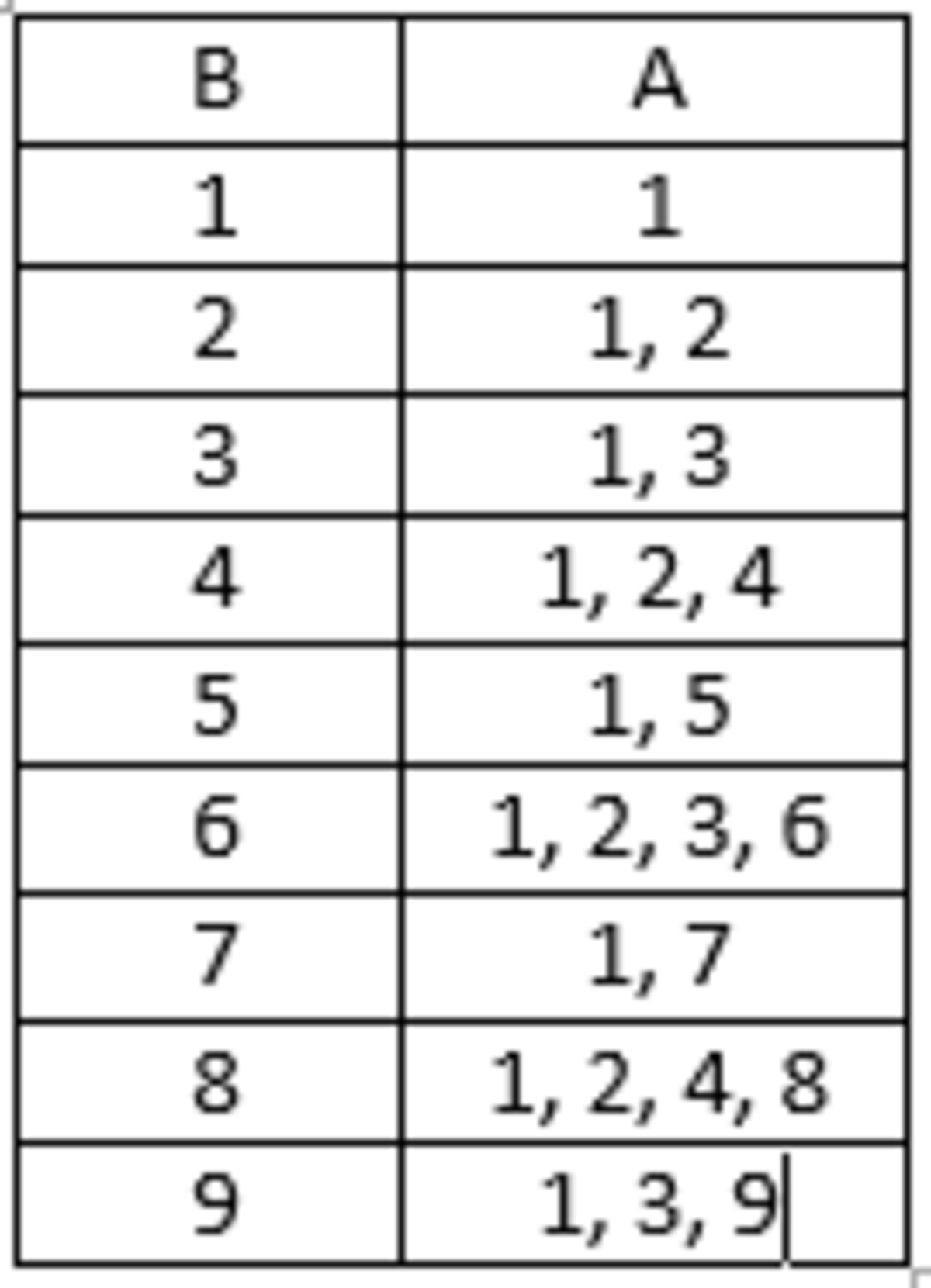
& all possibilities for second condition in tabulated form: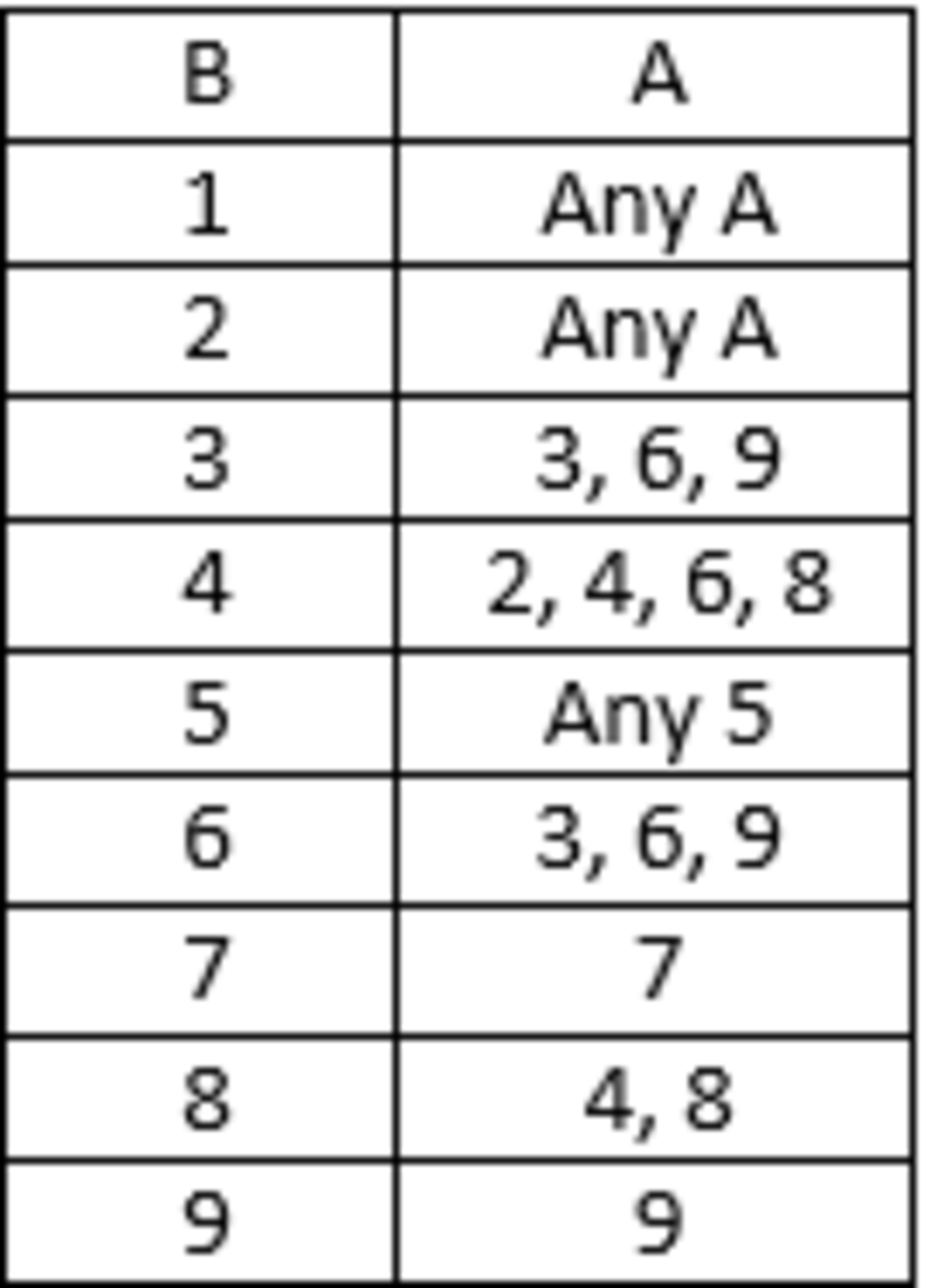
As, both conditions must be satisfied simultaneously so we have to choose only those combinations of A & B that are common in both the tables.
So, the numbers [AB not BA] are:
11, 12, 15, 22, 24, 33, 36, 44, 48, 55, 66, 77, 88, 99
Sum of these numbers is: 630