This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
19 solutions
Moderator note:
Good approach of determining A and E.
In fact, if we require that the units are distinct, then there is only 1 solution (up to permutation of B, C, D). Do you see why?
Your approach was similar to mine. I figured that the only way that was possible was A=6 and E=7, then used algebra and substitution to find B+C+D=19. They all added up to 32.
This is quite brilliant, though I find it quite funny that if there were no boundary of solutions, there could be several solutions such as A=3, B=1, C=2, D=6, and E=7, which would add up 19 , and 317+327+367 equals 2011. Haha math is fun!
Log in to reply
As I see it 317+327+367 only equals 1011. But Im not sure if it was some kind of math joke I didn't get...
BCD: can not be 627,687 or 697 because E=7...they should be 9,8 and 2
Log in to reply
he didn't said... BCD but 3 numbers , meaning ABE, ACE and ADE...
Yes, I did the same method - E = 7, and the maximum value of B+C+D+2 is 29 if they are identical, and 26 otherwise, so 3A +2 >= 20 and A < 7 must mean A = 6. From there it is as simple as:
300A + 10 (B + C + D) + 3E = 2011
=> 1800 + 10 (B + C + D) + 21 = 2011
=> 10 (B + C + D) = 190
=> B + C + D = 19
If A, B, C, D and E are all unique, then the only valid values of B, C and D are {2, 8, 9}
Because, 6 and 7 are already used. 8+5+4 only equals 18, so, 9 must be used, and among 8, 5, 4, 3, 2, 1, no pair of numbers adds up to 10 other than 8 and 2 to complete the 19. 682, 692, 622 is the only set of solutions. Though, as said, they could be any permutation. I worked with E first, but otherwise, was very close to Eli's solution, noting a maximum sum of BCD having a 2 carried, meaning 18 was needed as a sum for A+A+A+Carried = 20 as 15 was too small and 21 too big (and taken).
I used the same method !
A+B+C+D+E=1+2+3+4+5=15
➊ Ones: 3E = ?1, E = 7 and I carry 2 over the tens.
➋ Hundreds: 3A + carried from tens = 20 so A = 6 and carried from tens = 2 (7 is be too big and 5 is too small because we can’t have a carried of 5 from the tens)
➌ Tens: 2+B+C+D = 21 therefore B + C + D = 1 9
➍ A+B+C+D+E = 6+19+7 = 32
Additional note: Supposing that variables represent different digits, 9, 8 and 2 would replace B,C and D.
To determine those I start by using the 3 largest available number; 9, 8 and 5 which sum 22 so I have to lower the value by 3.
If I try to avoid 9 the 3 largest would be 8, 5 and 4 which sum only 17
If I try to avoid 8 the 3 largest would be 9, 5 and 4 which sum only 18
So the three numbers that sum 19 for B+C+D are 9, 8 and 2
That's what I did....fairly straight forward logic.
Right method. Good!
this is what i did too :D
u are right Achille 'Gilles' .this is the right solution to this problem .
step 1 : 3E = 1 or 11 or 21, solution is 21 if E = 7
step 2 : 3A + X = 20, X = 0 or 1 or 2, solution is X = 2 so 3A = 18, A = 6
step 3 : 2 + B + C + D = 21, so B + C + D = 19
step 4 : E + A + (B+C+D) = 7 + 6 + 19 = 32
ABC+ACE+ADE =2011, HERE THE LAST DIGIT IS 1 , IT MEANS IT MUST BE TWO DIGITS AND THE DIGIT MUST BE 3 EQUAL, THEN IT MEANS 21/3=7 BECAUSE LAST DIGIT MUST BE 1. NOW THE FIRST DIGIT MUST BE BETWEEN 20 THEN IT WOULD BE THE EQUAL PART, IT MEANS HIGHEST CAN BE 18. THEN ITS EQUAL DIGIT IS 18/3=6. SO WE CAN GET THE DIGIT A=6, E=7 . SO THE MIDDLE DIGIT MUST BE 21 MAXIMUM. BECAUSE THE LAST DIGIT IS 21 AND THE FIRST DIGIT IS 18 SO THE FIRST DIGIT WOULD BE 20-18=2 WHICH IS MIDDLE DIGIT FIRST DIGIT. AND THE LAST DIGIT FIRST IS 2 SO THE MIDDLE DIGIT MUST BE 21-2=19.
SO WE GET HERE A=6,E=7 AND B+C+D=19 => A+(B+C+D)+E=6+19+7=3
ABE+ACE+ADE=2011 LAST DIGITS E+E+E=21 FIRST DIGITS A+A+A=(20-2)=18
MIDDLE DIGITS B+C+D=(21-2)=19
A B E
A C E
A D E
20 21 1 (20-2) 21-2=19 21 18/3 21/3 A=6 B+C+D=19 7 => A+B+C+D = 6+19+7=32
Right, the point is that B+C+D=19
since 3E ends in 1, E must be 7 and we carry the 2. 3A + ? = 20 and the carry from the tens can only be 1 or 2 so the only thing that works is A = 6 we carried 2 from the ones and we need 2 in the hundreds so B + C + D = 19 so A + B + C + D + E = 6 + 19 + 7 = 32
adding the units digits we get 3E ends in 1 which means E=7 .
excluding units value we can get (10A+B) +(10A+C) +(10A+D) + 2 =201 {The 2 comes from the units sum}. simplifying ~ 30A +B+C+D=199 .
The maximum sum of B+C+D is (7+8+9) = 24 ; and minimum is (1+2+3) =6.
Hence, the equation 30A+B+C+D gives an inequality 175 < 30 A < 193. This makes A =6 since it is an integer.
Finally, 30(6) +B+C+D=199 giving B+C+D=19 .
A+B+C+D+E= 6 +19 +7 = 32
I'll be honest, I went with what "felt right" it was a guess that I was confident in and it was correct. I can't explain anything that got me to pick it
The maximum possible carry that can be generated on the leftmost side is 2 since 9+9+9=27 A+A+A=20 therefore 20/3=6.66 so A is 6 and 2 is carry from the 2 column which sum up to 20. Now B+C+D=21 we'll leave this here for a while. Now E+E+E=11 or 21, it cant be 11 for obvious reasons. So it is 21 and 21/3=7. So you have the values of A, B+C+D and E
Let 3E=21, then E=7. 3A must be equal to 18. Therefore B+C+D= 19 (21-2) where 2 comes as carry from 3E. So A=6, B+C+D=19, and E=7. The sum is 32
to have a sum of 2011, its must be a addition of 6 hundred plus numbers. So therefore, the Value of A must be 6 and last number which is E must be 7 because (7*3=21). Therefore there is a carry 2 the the (B+C+D) .Every random number you get to the addition of second digits ,you will get 19. So, 19+6+7=32.
only possible value of E is 7 and possible value of A is 6 so B+C+D=19 thus A+B+C+D+E=32
I did not write any equations. I did the problem by trial and error. Clearly, E must be 7, because it's the only single digit for which three of them comes out to a number that ends in 1 (21). This carries a two to the middle column.
Now, we see that A+A+A+x (where x is the number carried over from the middle column) must equal 20. A must be at least 4, because 3+3+3+9=18, which is less than 20, and any lower digit would have the same problem. If A is 4, x is 8 (to make 20), and B+C+D must equal (81-2), or 79. But you can't add three digits together to get 79, so we move on to 5. If A=5, x is 5, and B+C+D = (51-2), or 49, and we have the same problem. If A=6, x-2, and B+C+D = (21-2), or 19, and you can add three numbers together to get 19, so the answer is A(6) + B+C+D(19) + E(7), or 32.
Checking to make sure that there isn't another solution, if A is 7, 7+7+7 is 21, and we are already over the target of 20, and any higher digit would have the same problem, so there must not be another solution, assuming that each character represents a single digit. My solution is not dependent upon the individual values of B, C, or D.
I stared at it for a while, then just wrote a python script to brute force every possible combination and got 32 as the only solution. :)
Unit position total to end with 1.That must be 21.Hence E is 7.Tenth place also to end in 1.But 100th place total is 20.A must be 6. 3A is 18.Carry forward from tenth place must be 2.Sum of tenth place is 21.B+C+D is 19. A+B+C+D+E =6+ 19+7= 32
Let E=7 so 3E=21 which will generate carry 2 and let B=10,C=4,D=5 so B+C+D=19 + 2(carry)=21 which will again generate carry 2 , thenlet A=6 so, 3A= 3*6=18+2(carry)=20 so the result is=2011
B couldn't be 10, otherwise your solution is fine
Log in to reply
it should be B+C+D =19 and i think B,C,D could hold any value required for summing up into 19
E: 7 3=21 ie E=7, A: 20-2+6 3 ie A=6, B+C+D: 21-2+B+C+D ie B+C+D=19, So A+B+C+D+E=6+19+7=32
E+E+E=7+7+7=21; 2+B+C+D=21;so B+C+D=19; 2+6+6+6=20, Then A+B+C+D+E=6+19+7 = 32
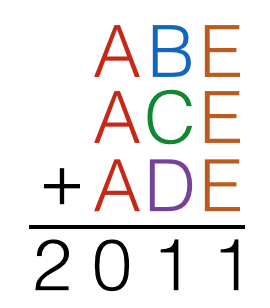

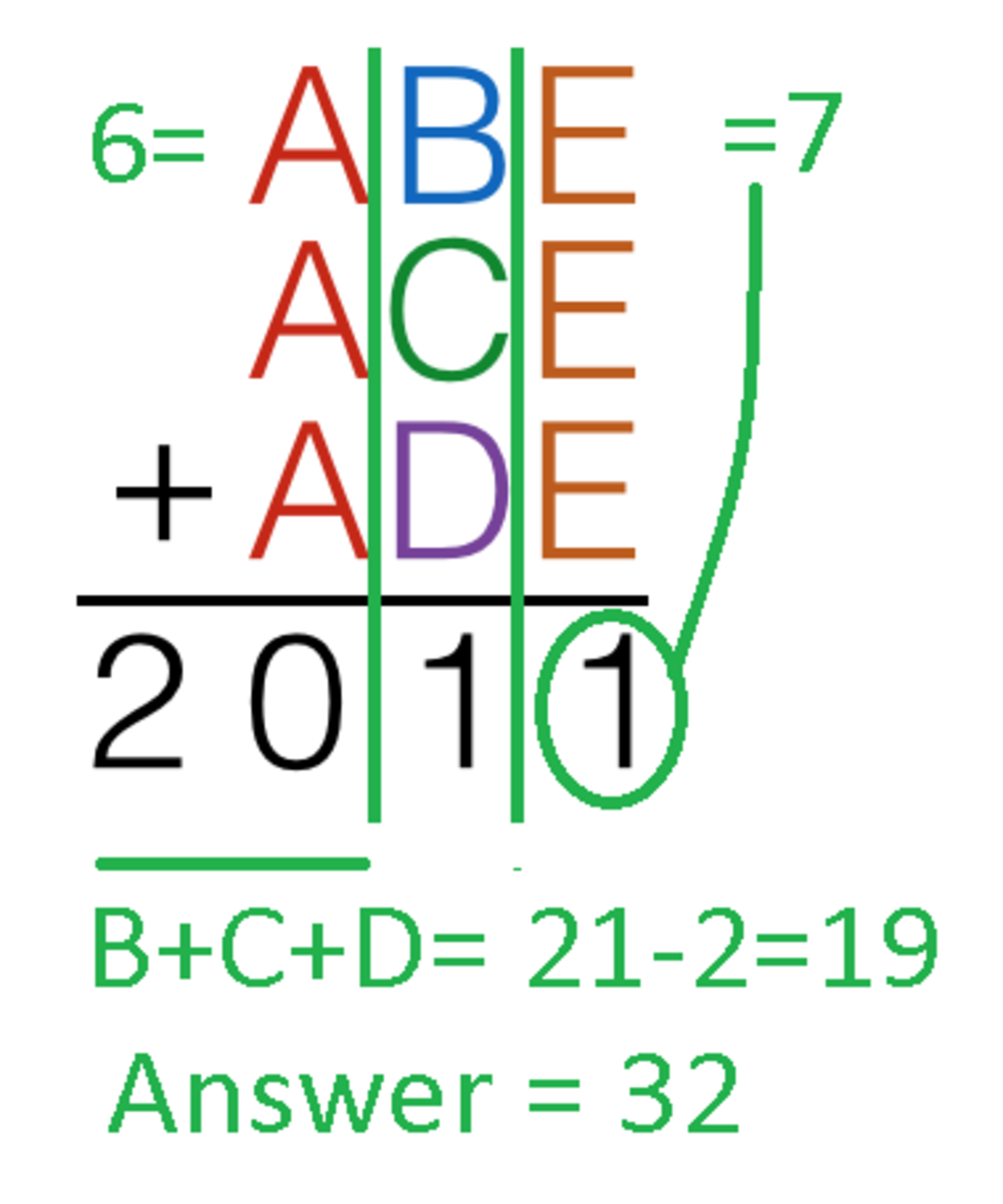
Note that all 3 numbers have the same hundreds digit, A . Since 6 0 0 ⋅ 3 = 1 8 0 0 and 7 0 0 ⋅ 3 = 2 1 0 0 , we must have A = 6 .
Note that all 3 numbers have the same units digit, E . Since E + E + E has a units digit of 1, we must have E = 7 .
Note that 6 B 7 + 6 C 7 + 6 D 7 = 1 8 0 0 + 1 0 ( B + C + D ) + 2 1 = 2 0 1 1 , so 1 0 ( B + C + D ) = 1 9 0 , so B + C + D = 1 9 . Thus, A + B + C + D + E = 6 + 1 9 + 7 = 3 2 .
To see that such numbers exist, we can take any B , C , D that sum to 19. As an example, the three numbers could be 627, 687, 697.