Number father
The pyramid of integers above is constructed in such a way that each "father" has exactly 3 "children": 1 → 2 3 4 , 2 → 5 6 7 , 3 → 8 9 1 0 , 4 → 1 1 1 2 1 3 , 5 → 1 4 1 5 1 6 , . . . . . . What number is the father of 2017?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
26 solutions
gotta love the detailed solution
Log in to reply
Thank you. Glad that you love it.
Log in to reply
It's simpler, honestly.
We can see that each row has:
N -> 3N-1,3N, 3N+1
We now have 3 equations where we must receive an integer.
1) I = 3N-1
2) I = 3N
3) I = 3N+1
If we sub I = 2017 in each equation, we get:
1) 672.67
2) 672.33
3) 672
Since equation 3 is the only integer, 2017 must be the latest born son of 672.
You can now solve for any year you want to know, without guessing who was born first.
Here is a very simple solution. To reach father's number , subtract one from number assigned to a third child and divide the remainder by 3 e.g. (4-1)/3=1 (13-1)/3=4; (16-1)/3=5; (2016-1)/3= 672
Log in to reply
That's what he did but he also explained why.
Also, (2016-1)/3 does not equal 672. But, more importantly, why did you choose 2016-1? Why not just 2016? Or 2016+1?
Sir which book is best for geometry from basic to high level. And i am big fan of your solution. Good day sir
Log in to reply
Sorry, I am not an academic. I am a retired person just an amateur math enthusiast. I don't use any textbook.
I'm not a mathematician... I 'just guess'..; But I merely intuited - there are four - not three - people involved... and divided each number by four - and chose the one without any remainder. Why or how this worked - ??? I have 'not idea'.... Luck????
Proof 2 isn't complete. you considered only one case. The first number of the generation a 1 , n . To generalize the proof: a 1 , n = 2 ( 3 n + 1 ) + i − 1
To reach the middle son of an arbitrary number we add to it the next numbers of the same row to reach the next generation plus the sons of the previous numbers in the same row to reach it's sons plus one to reach the middle son. M i d d l e s o n o f ( a i , n ) = a i , n + ( 3 n + 1 − i ) + 3 ∗ ( i − 1 ) + 1
Log in to reply
Thanks. I did consider the other cases. I put it in words instead of formula. I will change the solution.
Sorry, you were right. I did not consider other middle sons.
Let Ak be an arithmetic serie which represent the first children of each generation,Bk : the serie of 2nd children and Ck :of 3rd children : Ak=2,5,8,.............,k /Bk=3,6,9,12,.....k /Ck=4,7,10,13,........k (let n be the positive integer that represent the father of 2017 ) and k :the son (2017). We have 3 possibilities :1:2017 is the first child of n so it's an interger from Ak. /2: it's the 2nd child so it will be from Bk. /3: it's the 3rd son and it's from Ck. K=2+(n-1)3=3n-1 is the formula of Ak so : 2017=3n-1 /n=2018/3 (so 2017 isn't the 1st child of n because n must be a positive interger ) K=3+(n-1)3=3n is the formula of Bk so : 2017=3n /n=2017/3 (2017 also isn't the 2nd child of n ) K=4+(n-1)3=3n-1 is the formula of Ck so : 2017=3n-1/n=2016/3=672 (n=672 is a positive interger) So 2017 is the 3rd son of 672 and 672 is it'd father of course.
This makes more sense than the question. Would have probably made it to the right answer if the question wasn't so muddled.
Let N be a positive integer.
From the diagram above we obtain:
N → 3 N − 1 , 3 N , 3 N + 1 ⟹ 3 N − 1 = 2 0 1 7 , 3 N = 2 0 1 7 , 3 N + 1 = 2 0 1 7 ⟹ 3 N = 2 0 1 8 , 3 N = 2 0 1 7 , 3 N = 2 0 1 6 .
3 ∤ 2 0 1 8 and 3 ∤ 2 0 1 7 , but 3 ∣ 2 0 1 6 ⟹ N = 3 2 0 1 6 = 6 7 2 .
I think your solution is closest to mine. I went the simple route and guessed that division would get me close enough, so I divided 2017 by 3
Yes i believe you are right considering the direction of the arrows and g. But i wouldnt take this path since there are shorter ways to reach the final result.
The Number at tur right in every row is 1, 4, 13... The sequence keeps adding 3^n. Where n is every generation. The 7th generation to the right must be son Number 1+3+9+27+81+243+729=1093. Therefore er need 2017-1093=924 Sons to be born. Since every father had 3 Sons child Number 2017 must be son to father who is Number (1+3+9+27+81+243=364) PLUS a third of 924. 924/3=308.
2017's father must be Number 364+308=672.
Nice thinking. Very different approach.
Log in to reply
I did it this way too -- brute force method. not very elegant.
I did like that too :o
Me too - though I worked from the left, which made for bit of fiddling about with decimal fractions, as from the left, 2017 is in the 2015 'family'
I do it in the process you showed here
This was my first thought, but i came up with another idea before i solve it
Good thought
I took simple approach by noting that the middle number of each triad was thrice the parent. 2017 is not evenly divisible by 3 as its digits add up to 10. 2016's digits add up to 9 and so it is divisible by 3. So, 2017 would be the third child after 2016. And 2016 divided by 3 is 672.
I found the same pattern. The middle child is 3 times the father.
This was a really good explanation. Thanks!
While the sum of each 3 sons divided by their father gives 9, hence only 9 2 0 1 5 + 2 0 1 6 + 2 0 1 7 gives an integer which is 672
Brilliant! Simplest method by far.
Works for any year and any number of children
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
|
The father for 2017 is: 672
If x is the number who parentage we are trying to establish there are three possible outcomes on division of x by 3 left hand member of group has the solution ( n − 1 ) + 3 2 , the middle member is n + 0 and the right hand member is n + 3 1 where n is the value of the parent number so 3 2 0 1 7 = 6 7 2 3 1 tells us the value of the parent number is 672 and it is also a right hand member of the group
Why not just n-1/3 instead of (n-1)+2/3 is there an advantage to keeping it addition?
suppose,N is a positive integer.
as 1 is the main part of that number tree and except 1 each branches(supposing) gets 3 numbers accordingly.
so, for 2 0 1 7 ,this number will get = 3 2 0 1 7 − 1 = 6 7 2 as its branch
Look for a pattern. Each father has three children. The middle child is three times the father. The children are: 3 x father - 1, 3 x father and 3 x father + 1. 2017 is 3 x 672 + 1. So the father of 2017 is 627.
Notice that the middle children of every father are multiples of 3. In which the other siblings are either a +1 or -1 of that middle child. Hence, we shall investigate 2016 instead of 2017. Notice that the father is only a third of its middle child. Thus, leaves us to conclude that 3 2 0 1 6 = 6 7 2 is the father of 2017.
I found the same pattern. The middle child is 3 times the father.
For every parent P , the first child in its triplet is 2 P + ( P − 1 ) .
So to find the parent of 2017, we set 2 P + ( P − 1 ) = 2 0 1 7 and solve for the floor of P
⟹ P = ⌊ 3 2 0 1 7 + 1 ⌋ = 6 7 2
I noticed that for every father ending with 2 the son's end in 5 6 and 7, there for the answer had to end with a 2, which excludes all other possible answers, thus we arrive at the conclusion of 672.
The sons of 1 are 2,3 and 4 2+3+4=9 (1 × 9=9) The sons of 2 are 5,6 and 7 5+6+7=18 (2 × 9=18) The sons of 3 are 8,9,10 8+9+10=27(3 9=27) The sons of 5 are 14, 15, and 16 14+15+16=45 ( 5 9 = 45)
The middle no is multiple of three 2017 is not an multiple of three we can form a possible pair (2015,2016,2017) because nearest pairs do not include 2017 These pairs are :- [ ( 2012,2013,2014) and ( 2018,2019,2020) ]
2015+2016+2017=6048 their father's number is nine times smaller than them therefore:- 6048÷9 = 672 Thus, the father's no. is 672
With a tree in which each parent has the same outdegree (i.e. the branching factor is some constant b ) and where the nodes are numbered sequentially breadth-first from 1 to m, the parent of any node n is given by r o u n d ( b n ).
The first number of each triad divided by 3 gives the remainder 0.6666..., the second gives 0 and the third gives 0.3333, For example 14/3=4.6666, 15/3=5 and 16/3=5.3333 (where 5 is a father). As 2017/3 = 672.33333 then 672 is a father
1, (2, 3, 4), (5, 6, 7, 8, 9, 10, 11, 12, 13), (14,..,40), (41,…….,121), (122, ….., 364), (365,….,1093). (1094,…., 3280) 2017 – 1094 + 1 = 924, 924/3 = 308, 365 + 307 =672.
Just Divide the give number by 3 and round to nearest whole number:
P = ∥ 3 N ∥
i.e ∥ 3 2 0 1 7 ∥ = 672
The multiples of three are always the 'middle' number of each group of three years that share the same father. 2017 is not a multiple of three, but using rules of divisibility 2016 is (2+1+6 = 9). So 2016 must be the 'middle son' of (2016/3) = 672. As 2017 is one more, it must have the same father so hence the answer 672.
One the left, we can see that:
14/3=4.66 -> 5
15/3=5 -> 5
16/3=5.33 -> 5
If we we round up or down, we get the father number, which is true for the rest as well. Always divide by 3! This means that:
2017/3 = 672.33 -> 672!!
(Extra: since 2017/3 is bigger by 0.33, it means that 2016/3 is exactly 672, and 2015/3 will be 0.33 less than 672 - these are the numbers for the father 672 )
On the diagram, you notice that every middle child of every parent is 3 ∗ N where N stands for the value of the parent. By going through each answer, you come to the solutions 2013, 2016, 2019 and 2022. Each parent has two other sons, one either side of the middle child's number. 2 0 1 7 = 2 0 1 6 + 1 and from this we come to conclusion of 672.
By looking at the supplied tree, we can notice that each middle child is three times the number of the "father's" number. So if we just divide our child's number: 2017, by 3, we find out the number of the father and can even trace back the family tree of each number back to one. So 2017/3 = 672.3333333... The recurring 3 means that it is the oldest of the three children, so the siblings would be 2015, 2016, and our child 2017. If we were given child 2015, and we divided it by three, we get 671.6666666... repeating. This means that it is the first-born or first child. By taking the integer value of numbers that have a .66666 repeating, we have to add one to the integer part to get the father's number. So the father of 2017 is 672. 672 divided by 3 divides evenly so it must be the middle child, giving 224. 224 divided by 3 gives 74.6666666... which means 224's father is 75 and is the oldest or first child. 75 divided by 3 gives 25, even, so it is the middle child. 25 divided by 3 gives 8.333333... repeating, so his father is number 8, and is the oldest of the three children. Then the graphic tree supplied shows that child 8 has father #3, and is the middle child of father #1.
I saw the three sons, noticed that each row went up a power of three. I assumed I could solve the problem using ternary, but I don’t have a good enough understanding of the ternary number system, so I banked on finding the closest product to 2017. I don’t think this is a properly written solution, but the thought process helps.
We could potentially do 2017 divided by 3, but the problem is we don't know if 2017 is the middle, left or right child.
If it were the middle child, it would divide evenly into 3. We know it doesn't divide into 3 because the sum of the digits gives us 10 - which isn't divisible by 10.
Now the question is whether 2017 is the right child of parent x, or the left child of parent x+1.
Using the test for divisibility by 3 (sum the digits and check if the sum is divisible by 3), we note that the left children seem to give a remainder of 2 when the divisibility test for 3 is used. The right children give a remainder of 1.
Since 2017 gives a remainder of 1, we know 2016 must be the middle child, and dividing 2016 by 3 gives us the parent of 2017 - which is 672.
Hope that was easy to follow!
Another way to think of it is: The children follow this pattern: Left child, middle child (divisible by 3), right child, left child of next parent, middle child of next parent (divisible by 3), etc. So we only really need to know if 2017 is the number straight after the middle child (ie the number divisible by 3) or the number BEFORE the middle child. Since 2016 is divisible by 3, we know 2017 must be the right child. ie it shares parents with 2016. 2016 divided by 3 gives 672.
There is a pattern which the middle number is 3 times bigger than the father, and 2017 is not a multiple of 3, but 2016 is. That means the father number is 2016/3 which equals 672 then the number which comes after the 2016 is 2017.
Use the formula a*2+a-1 Where a is the father resulting the first son number Check for given number, 672 gives 2015 i.e. 2015, 2016 & 2017 are son of 672
Take the integer, subtract 1, and divide by 3. Ed Gray
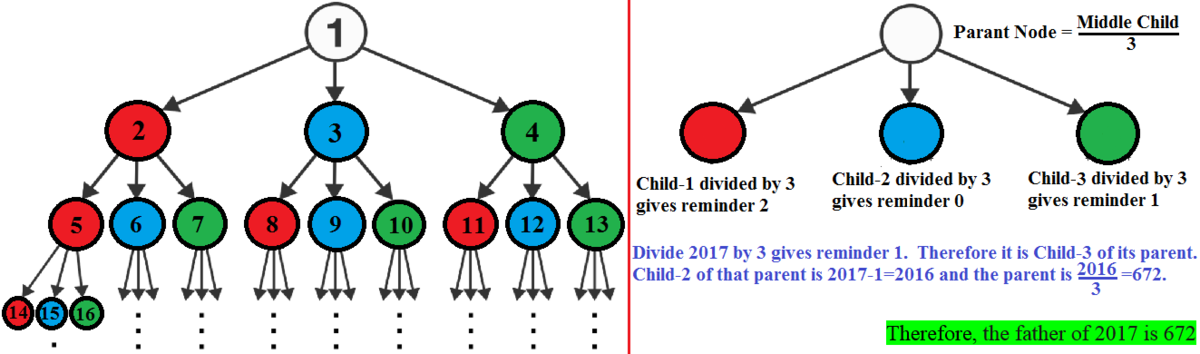
From the table, we observe that besides the first forefather 1, each family has three sons, the middle son is always a multiple of 3 (see proof 1). If the middle son is 3 n , then his father is n (see proof 2). Since 2017 is a prime it is not the middle son, but his elder brother 2016 is and 2 0 1 6 ÷ 3 = 6 7 2 is their father.
Proof 1:
Since the series starts with 1 and each family later always has 3 sons, the last son's number is always 3 k + 1 , where k is a positive number. Therefore, the middle son's number must be 3 k , a multiple of 3.
Proof 2: (Thanks, @Mohamed Hessien for his comments and the motivation for me to come up with a generalized proof.)
Starting from generation n = 0 , each row (generation) has 3 n numbers (sons). The last number of n th row is l n = k = 0 ∑ n 3 k = 2 3 n + 1 − 1 . Then the sequence number of k th member of n th row is a n , k = l n − 1 + k = 2 3 n − 1 + k = 2 3 n + 2 k − 1 . The middle sons are those having k = 2 , 5 , 8 , ⋯ , implying m n , i = a n , 3 j − 1 = 2 3 n + 6 j − 3 .
Now the sequence number of k th member of ( n − 1 ) th row, the father row, is given by a n − 1 , k = 2 3 n − 1 + 2 k − 1 . Multiplying by 3, we have: 3 a n − 1 , k = 2 3 n + 6 k − 3 = m n , k ■