Number Game Theory
Jonathan and Peter are playing the Number Game . It is a game where one of the players try to guess a four-digit number that is secretly written by a "number dealer" in the least number of guesses possible. There are a few rules to consider though.
- No two digits can be equal.
- None of the digits can take a zero value.
- For every turn that a player tries to guess the four digit number, the number dealer will give the player two numbers. The first number gives the number of correct digits that are in the correct position, while the second number gives the number of correct digits in the wrong position.
- The dealer cannot give any other information about the number (if it is odd/even, prime, perfect, etc.)
Jonathan dealt a four digit number to Peter. Peter guessed for the number four times, and obtained the following results:
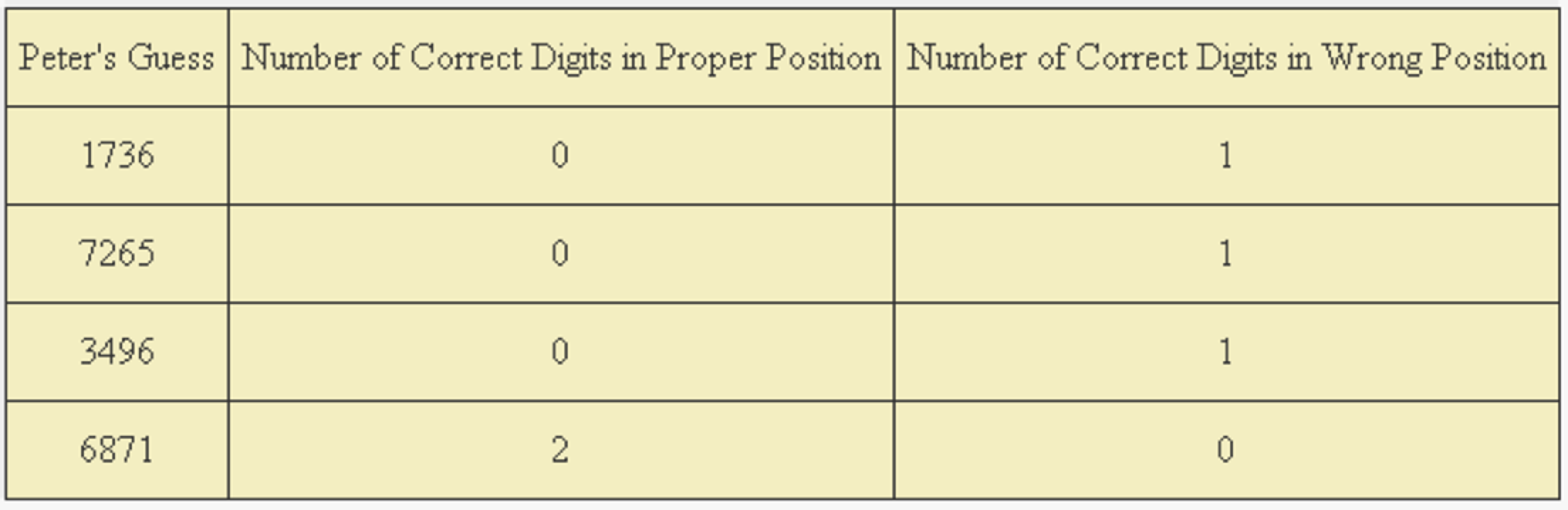
What is the smallest number that Jonathan could have written?
Note: This problem is original.
The answer is 2841.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
I hope this solution is worth reading. :)
Let C ( x ) be the number of correct digits in the proper position (place value) for a four-digit number x that satisfies the given criteria. In a similar fashion, let W ( x ) be the number of correct digits in the wrong position.
It is important to note that
C ( x ) + W ( x ) ≤ 4 .
In the problem, C ( x ) = 2 when x = 6 8 7 1 . Thus, there are ( 2 4 ) = 6 possibilities with which two digits from this number are correct.
Enumerating these possibilities, we have
A = 6 8 p q
B = 6 p 7 q
C = 6 p q 1
D = p 8 7 q
E = p 8 q 1
F = p q 7 1
Now, we will determine the "eligibility" of each of the possibilities. For example, if the number we're looking for is of the form F , then W ( 1 7 3 6 ) = 2 , which is a contradiction. Thus, the number we're looking for cannot be of the form F .
The same thing would go for form B , as if such is the case, then W ( 1 7 3 6 ) = W ( 7 2 6 5 ) = 2 , which is false.
The same thing would go for form C , as if such is the case, then W ( 1 7 3 6 ) = 2 , which, then again would be another contradiction.
And so we are left with three possibilities, namely A , D , and E . Let us investigate each one.
If the number we're looking for is of the form A , that is 6 8 p q , then it should satisfy both C ( x ) and W ( x ) for the four numbers guessed by Peter. By this we could determine what values p and q could assume.
For x = 1 7 3 6 , W ( x ) = 1 and C ( x ) = 0 . Since 1 7 3 6 and 6 8 p q both have 6 in common, then we can assume that p and q cannot be 1 , 7 , and 3 .
In a similar way, for x = 7 2 6 5 , it can be deduced that p and q cannot be 7 , 2 , and 5 .
Furthermore, for x = 3 4 9 6 , it will be deduced that p and q cannot be 3 , 4 , and 9 .
Summing it up, if the number we're looking for is of the form A , that is 6 8 p q , p and q can not assume any of these values { 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 } . Hence the number we're looking for is not of the form A .
We have narrowed down our options to two possibilities, D and E .
If we check option D for x = 1 7 3 6 , we find out that p and q cannot be 1 , 3 , and 6 .
On the other hand, if we check option D for x = 7 2 6 5 , we find out that p and q cannot be 2 , 5 , and 6 .
Meanwhile, if we check option D for x = 3 4 9 6 , we find out that no two digits coincide with D = p 8 7 q . Since p and q cannot be 3 or 6 , then either p or q could be 4 or 9 , but not both. This is because if p = 4 , and q = 9 or vice versa, then W ( 3 4 9 6 ) = 2 , which is false.
However, if p = 4 or p = 9 , q could not take any other value, thus eliminating option D .
We have totally narrowed down our choice to option E , whose form is E = p 8 q 1 .
If we check option E for x = 1 7 3 6 , we find out that p and q cannot be 3 , 6 , and 7 .
On the other hand, if we check option D for x = 7 2 6 5 , we find out that p and q cannot be 6 and (\7), and that either p or q could be 2 or 5 , but not both.
Meanwhile if we check option E for x = 3 4 9 6 , we find out that p and q cannot be 3 and 6 , and that either p or q could be 4 or 9 , but not both.
The number of values that p and q can assume is the number of ordered pairs that can be taken from this set { 2 , 4 , 5 , 9 } minus the ordered pairs ( 2 , 5 ),( 5 , 2 ),( 4 , 9 ), and ( 9 , 4 ).Thus, the total permutations for the values of p and q equals 4 P 2 − 4 = 8 .
These 8 permutations give the numbers
2 8 4 1
2 8 9 1
4 8 2 1
4 8 5 1
5 8 4 1
5 8 9 1
9 8 2 1
9 8 5 1
So the answer to the question is 2 8 4 1 .
Feel free to ask me questions. Thank you for reading!