Number Grid Puzzle
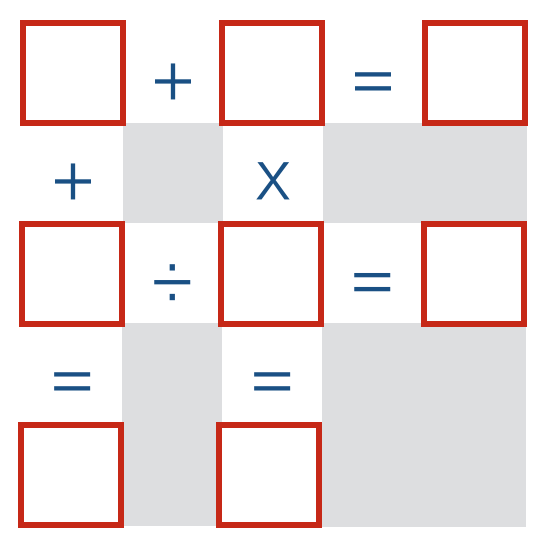 Place each of the digits
1
,
2
,
3
,
…
,
8
in the grid above so that all of the equations are true.
Place each of the digits
1
,
2
,
3
,
…
,
8
in the grid above so that all of the equations are true.
Give your answer as the numbers from left-to-right and then top-to-bottom. For example, if you filled in the grid (incorrectly) as shown below, your answer would be 3 2 5 4 1 8 7 6 .
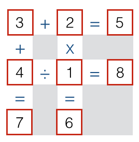
The answer is 14562378.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
By logic, no. 1 cant be in any places except A, Being in B means the multiplication will fail, and in D means the division makes a fraction.
Well, i don't used that First, i see that D must be even But D can't be 8 (because A+D>=9, which false) or 4 (2 2 or 4 1, both of them are incorrect) or 2 (like 4), so D must be 6 If D is 6 then E=2 or E=3, if E =3 then B D=3 (false) or B D=6 (false) or B*D>=9, false, therefore, E must be 2 So F=2 If E=2, the only number multiply to 2 <9 and diffent with other is 4, so B=4 From now we can easily fill all the rest
Let answer = a = ? ? ? ? ? ? ? ? with each ? being a different single digit number.
First we find out what can go in box 1 .
Every number except 8 can go in box 1 since having 8 in that box will make boxes 3 and 7 at least 9 which isn't on the list.
Next is box 2 .
Only 2 , 3 and 4 can go in this box. 1 can't go here because that would make two numbers in the multiplication line the same. Anything above 4 can't go here because the other box in the multiplication line must be at least 2 .
With this we can reduce the possible numbers for box 1 since 7 is no longer possible as it would require box 2 to be equal to 1 which it can't be.
Thirdly box 3 .
Every number except 1 and 2 can go here. Having 1 or 2 here would mean either a number has to be repeated or a number not on the list must appear (e.g 0 or − 1 ).
Fourthly box 4 .
Only 6 can go here since it's the only number in the list with a set of factors which are different numbers and do not contain 1 . 8 doesn't count as it can't be in either of the addition lines, since this box is in an addition line it can't contain 8 .
So a = ? ? ? 6 ? ? ? ?
This further reduces the possible numbers for box 1 to being either 1 or 2 since anything higher would make box 7 contain a number above 8 .
Along with reducing the possible numbers for box 1 , this also reduces the possible numbers for box 3 to 3 , 4 , and 5 . 6 isn't an option since we're already found where 6 goes.
Next is box 5 .
Only 2 and 3 can go here since box 4 has been found to be 6 and 6 only has factors of 2 and 3
Onto box 6 .
Only 2 and 3 can go here since we're working with the factors of 6 .
Box 7 is next.
Only 7 and 8 can go here since it must be above 6 due to box 4 being equal to 6 .
Finally box 8 .
Only 8 can be put here as any other combination would result in multiple of the same number on the grid.
So a = ? ? ? 6 ? ? ? 8
Now onto the fun part.
The only two numbers which make 8 when multiplied together - which are also in the list - are 2 and 4 .
From this we can determine that box 2 must be 4 and box 5 must be 2 since the only box in the multiplication line which could be 4 was box 2 which leaves box 5 to be 2 .
So a = ? 4 ? 6 2 ? ? 8
This reduces most of the possible numbers for some of the boxes.
Box 1 can now only be 1 since 2 is already on the grid.
So a = 1 4 ? 6 2 ? ? 8
This makes box 3 equal to 5 and box 7 equal to 7 .
So a = 1 4 5 6 2 ? 7 8
The only number left is 3 which means it goes in box 6 .
a = 1 4 5 6 2 3 7 8
Hope this helped.
Its lengthy but understandable!
There are two possible combination of numbers in second row, first is (6,3 and 2) and second (8,2 and 4). You need to find out which of these two combinations is suitable. After finding out, you can easily solve for the other numbers in the boxes.
I agree that a lengthy explanation isn't necessary. Following from what you said (or what George Nasry said), A,C, and G have to be 1, 5, and 7 (in some order) and therefore the two sums must be 1+4=5 and 1+6=7. But we can't have
6 * _ = _
and the rest follows easily.
Obviously, the button two are seven and eight (why, you ask?). That makes the second row 6:3=2 or 6:2=3. The first one cannot be (y x 3 = 8!!). We are done.
1+4=5, 6/2 = 3, 1+6=7, and 4*2=8
First, I started with multiplication process, it's logically to be either 2x4=8 or 2x3=6 then dividing it must be number by 2, by putting 1 in the upper left square, you can fit the rest numbers very quickly
1 does not go in the product nor division because we would have to repeat a number. Its not a result either. Then it goes in the top left, or in (1,1)=(1st row,1st column). Since results cannot exceed 8, the only pairs allowed for the product are 4,2 and 3,2. If 2 were placed in (1,2) then 3 would go in (1,3) and that forces us to use 4 as a denominator making 8 be in (3,2). But we have to get an integer when dividing by 4 and the only possibility is to have 8 in (2,1). This cannot happen. Then 2 goes in (2,2).
Now, an even must go in (2,1). It's not 8 because 8 is not a factor of anything and its not 4 because numbers don't repeat. Then its 6. I believe now it's pretty easy to solve at this point.
- We start with second row the division, the second item can't be 1 since it will cause the multiplication of the second column to be have the same number as result, so for division result to be an integer between 1 and 8 we have left 4:2 ( which is discarded as answer is 2 which will cause the use of 2 twice) or 6:2 or 6:3( which is discarded also since the multiplication of the second column will be out of set) or 8:4 ( which is discarded also since any number we add to eight in first column will be out of set) so we are left with 6:2, so second row is 6:2=3
- Then we go to first row clearly we can't have 1 as result so it must be on first row and it can't be the second number as it will cause multiplication of second column to use same number twice. So 1 has to be the first number, which lead the third row first number to be 7, so we have left now 4,5 and 8 and it is trivial that first row is 1+4=5 and second row 6:2=3 , first column 1+7 =8 , second column 4x2=8
I used this logic:
Placing the number 1:
The number 1 can't be in the square E, because you will have a division or a multiplication by 1, and the number in squares F and H will be the same of squares D and B respectively, which is not allowed.
The number 1 can't be also in the squares C, F, G and H because the other numbers are large than 1 to result in 1. In square B the multiplication will not work, and in the square D we'll have a fraction.(Observation by Moustafa El-Sayed) Thus the number 1 will be in the square A
Placing number 2:
The number 2 is the only number that you can put in square E because the other numbers, except the triplet 2, 4 and 8; are coprime integers. Thus you have the number 2 in the square E, the number 4 in square B and the number 8 in square H, because this triplet is the only that these 3 numbers aren't coprime integers excluding the number 1. So, the multiplication will be done correctly.
Placing the other numbers:
Using the remaining numbers (3, 5, 6, 7) to match the multiplication, you only have one way, which is placing the number 6 in square D and the number 3 in square F.
To solve it you place the remaining numbers in they respective places, which are the number 1 in square A, number 5 and 7 in the squares C and G respectively.
The final board is this: