Number of onto functions ?
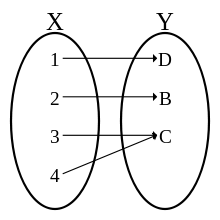 Let
and
.
Let
and
.
A function be defined from to .
If, & ,
then what is the number of onto functions defined from to ?
Note:
The figure (in the pic) is a rough one. :)
Wanna try more problems on functions ?
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
With f ( x 1 ) = y 1 and f ( x 2 ) = y 2 we must have each of y 3 , y 4 mapped onto by at least one element of S = { x 3 , x 4 , x 5 } for f to be an onto function.
We then have two scenarios to consider:
(i) One element of S maps onto either y 1 or y 2 and the other two elements are mapped onto { y 3 , y 4 }. As there are 3 elements in S , 2 elements in { y 1 , y 2 } and 2 ways in which an onto function can be mapped between two 2 -elements sets, the number of possible onto functions in this scenario is 3 ∗ 2 ∗ 2 = 1 2 .
(ii) All the elements of S are mapped to { y 3 , y 4 }. The are 2 3 = 8 ways in which the elements of S can be mapped, two of which result in them all being mapped to either y 3 or y 4 . Thus there are 8 − 2 = 6 onto functions possible in this scenario.
The total number of onto functions under the given conditions is therefore 1 2 + 6 = 1 8 .