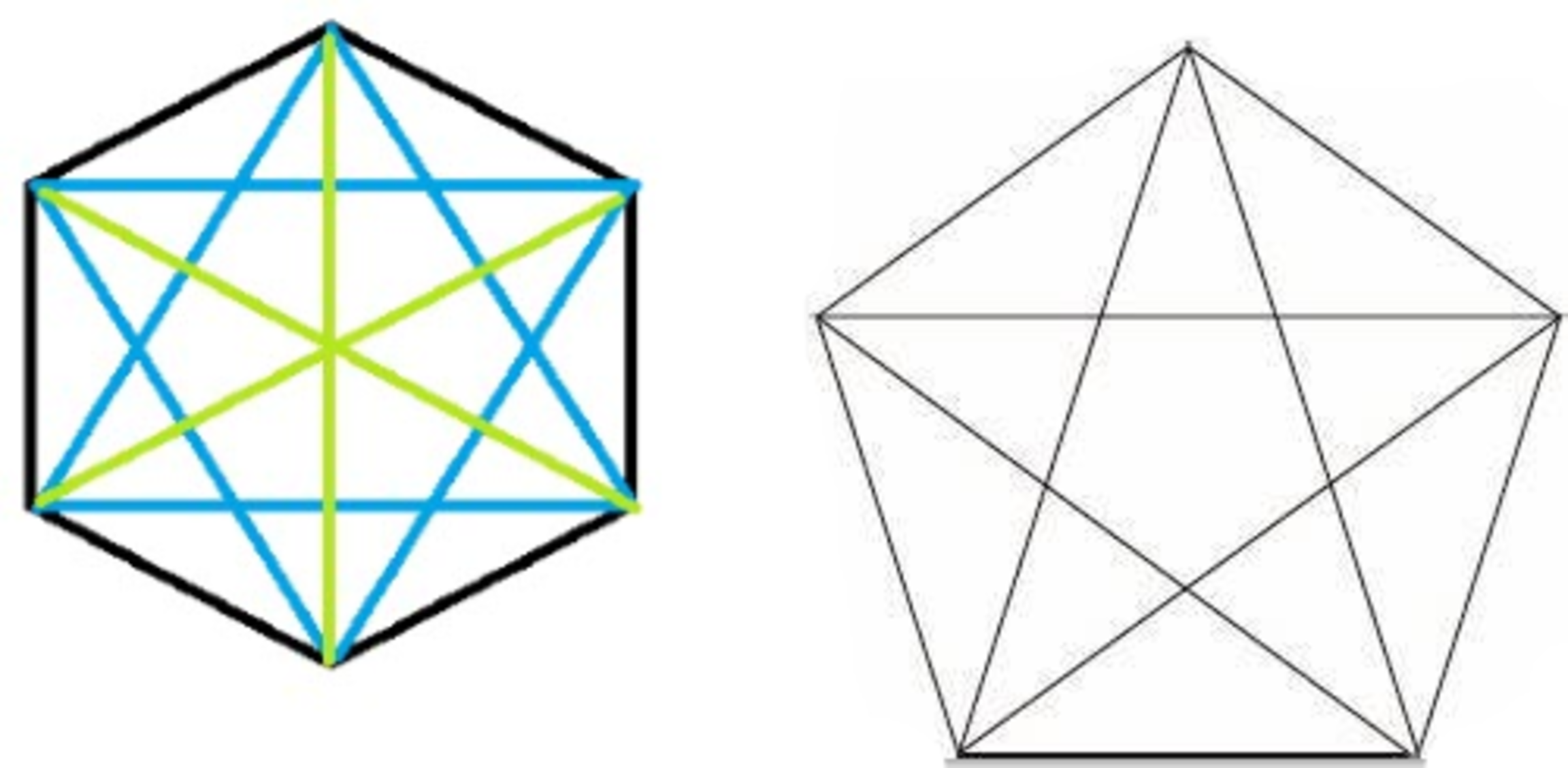
Number of Parallel Diagonals

All the diagonals of $n-polygon$ (where $n>6$ ) is parallel to at least one other diagonal.
[For proof, we can observe that triangles and quadrilaterals does not have any diagonal parallel to one of its sides. And when $n>6$ every diagonal divides the polygon into $2$ parts at least one of which is not a triangle or quadrilateral. So there is at least one diagonal parallel to that diagonal]

An $n-polygon$ has $^{n}C_{2}-n$ diagonals.

So $101-gon$ has $\frac{101*100}{2}$ $-101=4949$ diagonals and $100-gon$ has $\frac{100*99}{2}$ $-100=4850$ diagonals.

So the difference is $4949-4850=99$