Number of Paths in a Road-Map!
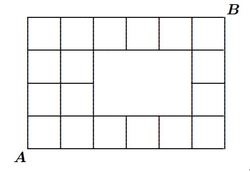In the road-map shown in the diagram above, each line segment represents a street which can only be traveled along in either the upwards or the rightwards direction. How many paths are there from point
to point
?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
If we choose any intersection, how many paths are there to get to it? Well, to get to any intersection, we must come from directly to the left or directly below. Thus, the total number of paths to any intersection is the sum of the number of the paths to the intersection immediately to the left and the number of paths immediately below.
Look at the above figure. As an example, let's consider the bottom left corner. To get to the intersection directly above A , there is only one path. To get to the intersection directly to the right to A , there is only one path. To get to the intersection 1 move up and 1 move right of A , there are 2 paths - 1 each through each of the two previously mentioned intersections.
We can follow this line of reasoning to fill in the number of paths to any intersection on the grid.
Hence, there are 80 paths from A to B .
This is a solution based on Logical Aptitude. This problem can also be solved using Combinatorics. If you have an elegant solution to this problem using Combinatorics, please share it.