Number of rectangles
Probability
Level
4
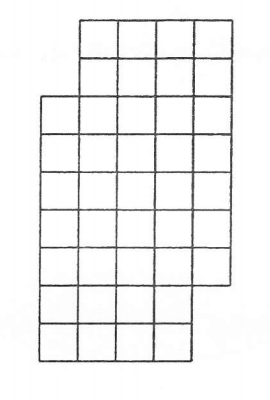
Find the number of rectangles that can be formed from the gridlines of the board as shown in the figure above.
This is a part of the Set .
The answer is 509.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
It was finished in a twinkling. The script builds the full rectangular lattice then removes the four points at the corners. Then it samples 4-combinations of lattice points. It tests whether the four points form a rectangle by calculating the sizes of their sets of x- and y-coordinates.