Multiplication to Exponentiation
2 x = x 2
How many distinct real values of x satisfy the equation above?
Details and Assumptions :
- You are recommended to solve this problem without graphing the two equations.
Check out more problems. So, try the set : Can you draw its graph ?
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Can it be done without drawing graphs?
Log in to reply
yes , offcourse it can be done without using graphs too. !!!
Log in to reply
I tried with logarithm method, I am not getting value, can you please try once.
Please give non-graphical solution
what is the negative value?
Since no one plots the two curves 2 x and x 2 , I am showing it here. I used Excel spreadsheet to plot this.
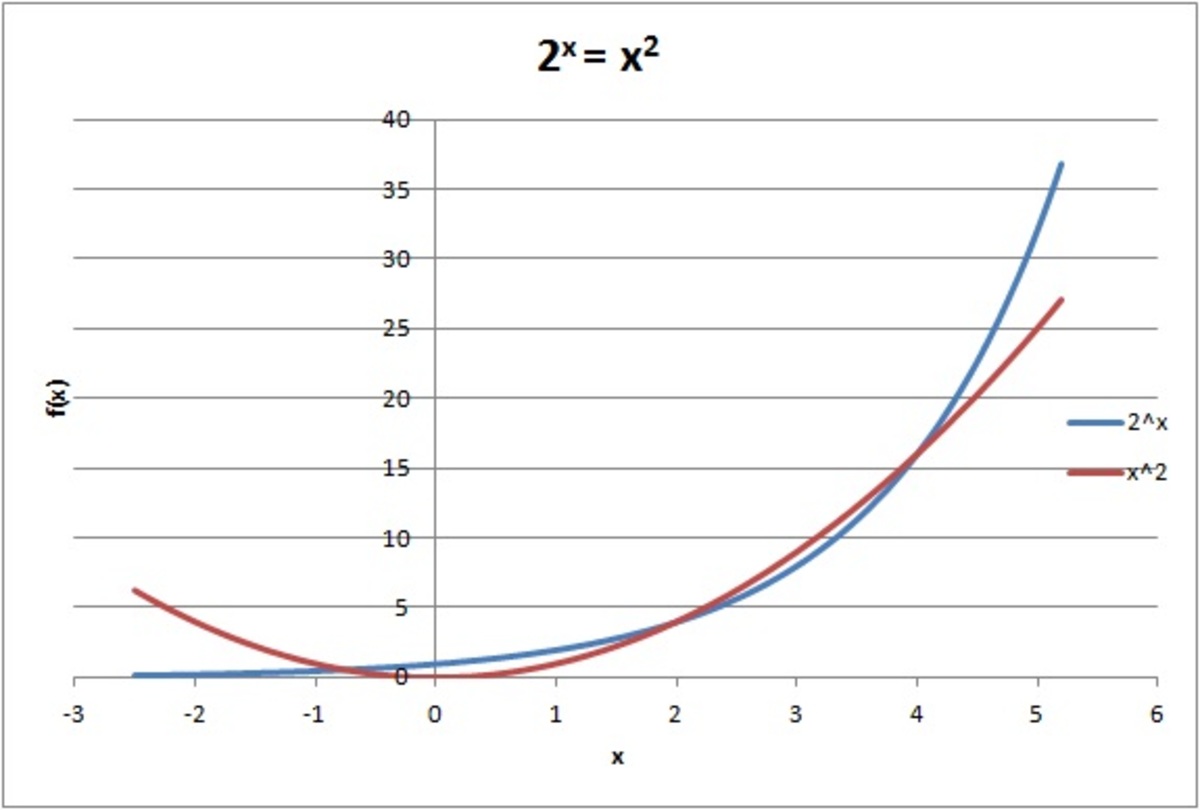
The two curves cut at three points at x ≈ − 0 . 8 , x = 2 and x = 4 and therefore, there are 3 distinct real solutions.
What would be the algebrical solution
Let's change this problem 2^x = x^2 for what x? into a function: f(x) = 2^x - x^2 Now the question is, for what x is f(x) = 0; or, what are the roots of f(x)? The Newton-Raphson method starts with some first guess, x[0], and finds the next guess, x[1], by a formula. Then, using this guess, we apply the same formula to find a new guess, x[2]. We continue until we're as close as we wish. The formula is x[i+1] = x[i] - f(x[i])/f'(x[i]) We need f'(x), the derivative of f(x). It is f'(x) = 2^x * ln(2) - 2x Thus the formula for our problem is x[i+1] = x[i] - (2^x[i]-x^2)/(2^x[i]*ln(2)-2x) You can set this up in a spreadsheet. Then try different first guesses x[0]. You'll find that the algorithm zeroes in on one of the three roots, depending on the starting value. If I start with x[0] = 0, I get the root: x = -0.766664696 after 5 iterations. You can verify: 2^-0.766664696 = 0.587774756 (-0.766664696)^2 = 0.587774756 If I start with x[0] = 1, I get the root x=2. If I start with x[0] = 3, I get the root x = 4. You have observed that there are three roots.
You might like to use sage on https://cloud.sagemath.com.

While manipulating, I came across this:
s
ss
Can anyone explain this difference? Apparently the negative root disappeared because of the requirement for x to be positive for that alternative form. But why is there such a requirement?
@John Muradeli Taking lo g ( x 2 ) = 2 lo g x assumes the positive value of x .
Log in to reply
Why, because x < 0 will yield undesired results for 2 lo g x ?
1 0 y = x 2 v. 1 0 y / 2 = x
Second is the square-root of the first. The positive root. Why the positive? Because your co-domain is real? No. The first one's real inputs yield real outputs. This is because the argument remains positive, whereas in the transformation the argument can be negative. So I guess the proper way to transform would be lo g x 2 = 2 lo g ∣ x ∣ , now, wouldn't it?
 s
s
This'll do.
P.S. - how do I center my non-LaTeX text?
I want to insert an image in my solution from my computer how can I do it
@Rocel Polintang 2 0 = 0 2 because 1 = 0 .
If we draw the graphs of the two expressions i.e. y= 2 x and y = x 2 , then their graphs will cut each other at three distinct points, so the given equation 2 x = x 2 has 3 solutions. two values of x are x=2 and x=4 and one value of x will be negative..