Can you draw its graph? 3

It is given that:

$e^x = x^3 \quad \Rightarrow \quad x = 3\ln{x}$

Computing for $3\ln{x}$ for $x = 1, 2, 3 ... 10$ and listing them as follows:

$\space x \quad \quad 3ln(x) \quad \quad x-3ln(x)$

$\space1 \quad 0\quad \quad \quad \quad \quad \quad 1$

$\space2\quad 2.079441542 \quad -0.079441542$

$\space3\quad 3.295836866\quad -0.295836866$

$\space4\quad 4.158883083\quad -0.158883083$

$\space5\quad 4.828313737\quad \space \space 0.171686263$

$\space6\quad 5.375278408\quad \space \space 0.624721592$

$\space7\quad 5.837730447\quad \space \space 1.162269553$

$\space8\quad 6.238324625\quad \space \space 1.761675375$

$\space9\quad 6.591673732\quad \space \space 2.408326268$

$10\quad 6.907755279\quad \space 3.092244721$

It can be seen that $x > 3\ln(x)$ when $x = 1$ but $x< 3\ln{x}$ when $x = 2$ , then $x > 3\ln(x)$ again when $x = 5$ and the difference increases after that. Therefore, there are two values of $x$ that satisfy $e^x = x^3$ , one $1<x<2$ and the other $4<x<5$ .

Since a graph is requested, I am attaching the $f(x) = e^x-x^3$ graph here. It clearly shows that there are $\boxed{2}$ real solutions when $x \approx 2$ and $x \approx 4.5$ .

Just for curiosity, considering the properties of the Lambert W function, i tried to get the number of solutions.

$e^x=x^3$

$(e^x)^{-\frac{1}{3}}=(x^3)^{-\frac{1}{3}}$

$e^{-\frac{x}{3}}=x^{-1}$

$xe^{-\frac{x}{3}}=1$

$-\frac{x}{3} e^{-\frac{x}{3}}=-\frac{1}{3}$

$W(-\frac{x}{3} e^{-\frac{x}{3}})=W(-\frac{1}{3})$

$-\frac{x}{3} =W(-\frac{1}{3})$

$x =-3W(-\frac{1}{3})$

Then....

$W(x)$ , for:

• $x<-\frac{1}{e}$ gives 0 real solution;

• $x=-\frac{1}{e}$ , $W(-\frac{1}{e})$ =-1 (1 solution);

• $-\frac{1}{e}<x<0$ gives 2 real solutions;

• $0\le x$ gives 1 real solution.

As $-\frac{1}{e}<-\frac{1}{3}$ , we have 2 real solutions.

Clearly, there are no solutions $x\leq0$ . For positive $x$ , the equation is equivalent to $x=3\ln(x)$ or $f(x)=x-3\ln(x)=0$ . Now $f'(x)=1-3/x$ so that the graph of $f(x)$ is increasing for $x>3$ , decreasing for $x<3$ , and concave up throughout. The global minimum of $f(x)$ is attained at $x=3$ , with $f(3)<0$ . Since $\lim_{x\to\infty}\ f(x)=\lim_{x\to{0^+}} f(x)=\infty$ , the given equation has two solutions, by the intermediate value theorem.

One solution is easy to imagine around 2 and because of the fact that rate of increment of e^x is much more than x^3 when x-.>large value => somewhere the graph of e^x will go above the graph of x^3 Which means they will cross each other => 2 real solutions

For x < 0, $e^x > 0$ and $x^3 < 0$ , i.e., no roots before 0. After 0, the derivative of $x^3$ starts bigger then the derivative of $e^x$ , but the value of $e^x$ itself starts bigger then $x^3$ , and it means that there are or 0, 1, or 2 roots, if e^x is always bigger then x³, if e^x is bigger or equal to x³ or if there. It's easy to see that $e^2 < 8$ , then 2 roots.

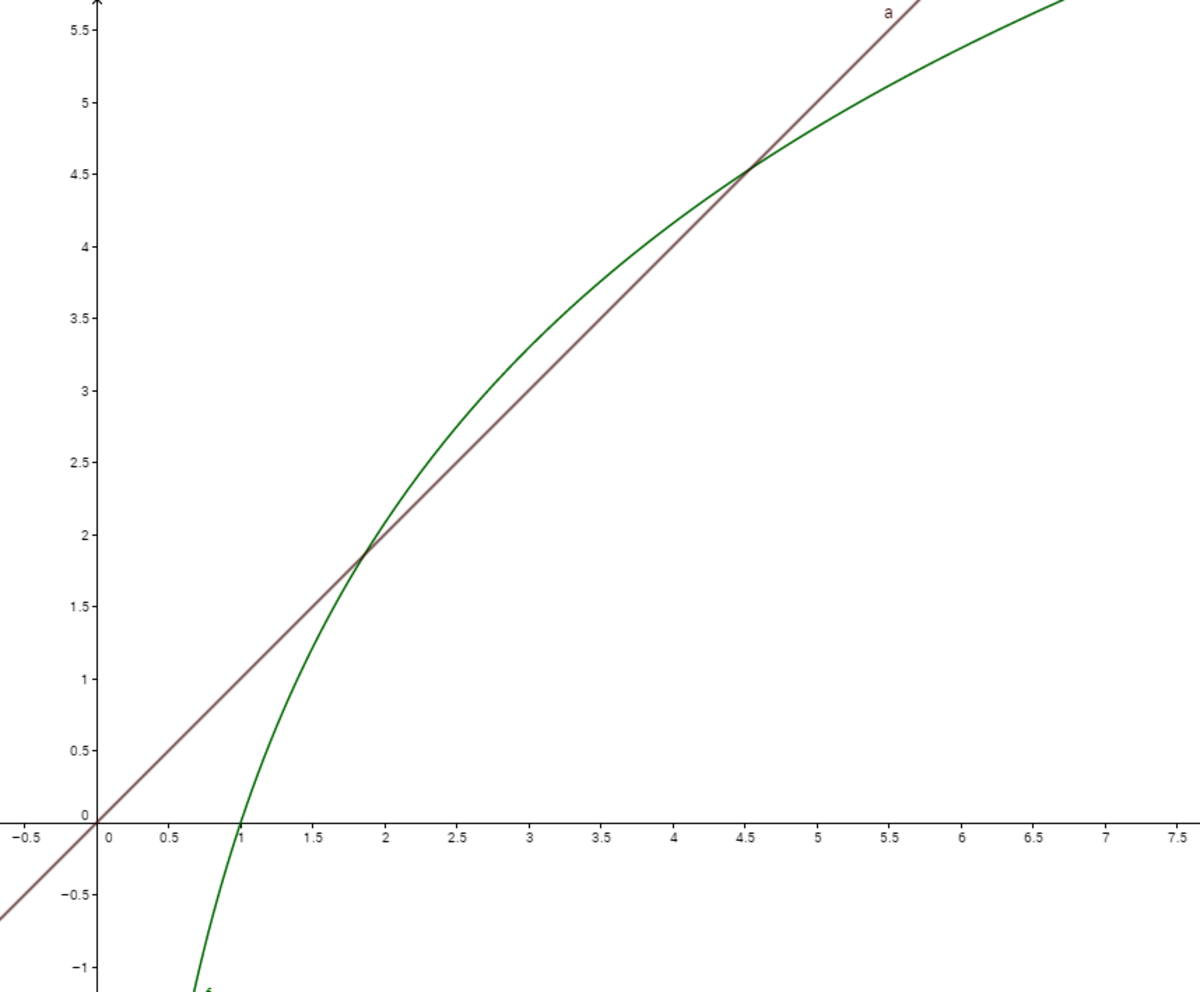
Rewrite as $x = 3\ln{x}$ . This is the graph: $\boxed{2}$

Let Z be the set of integers e^x=x^3 x=3ln(x)

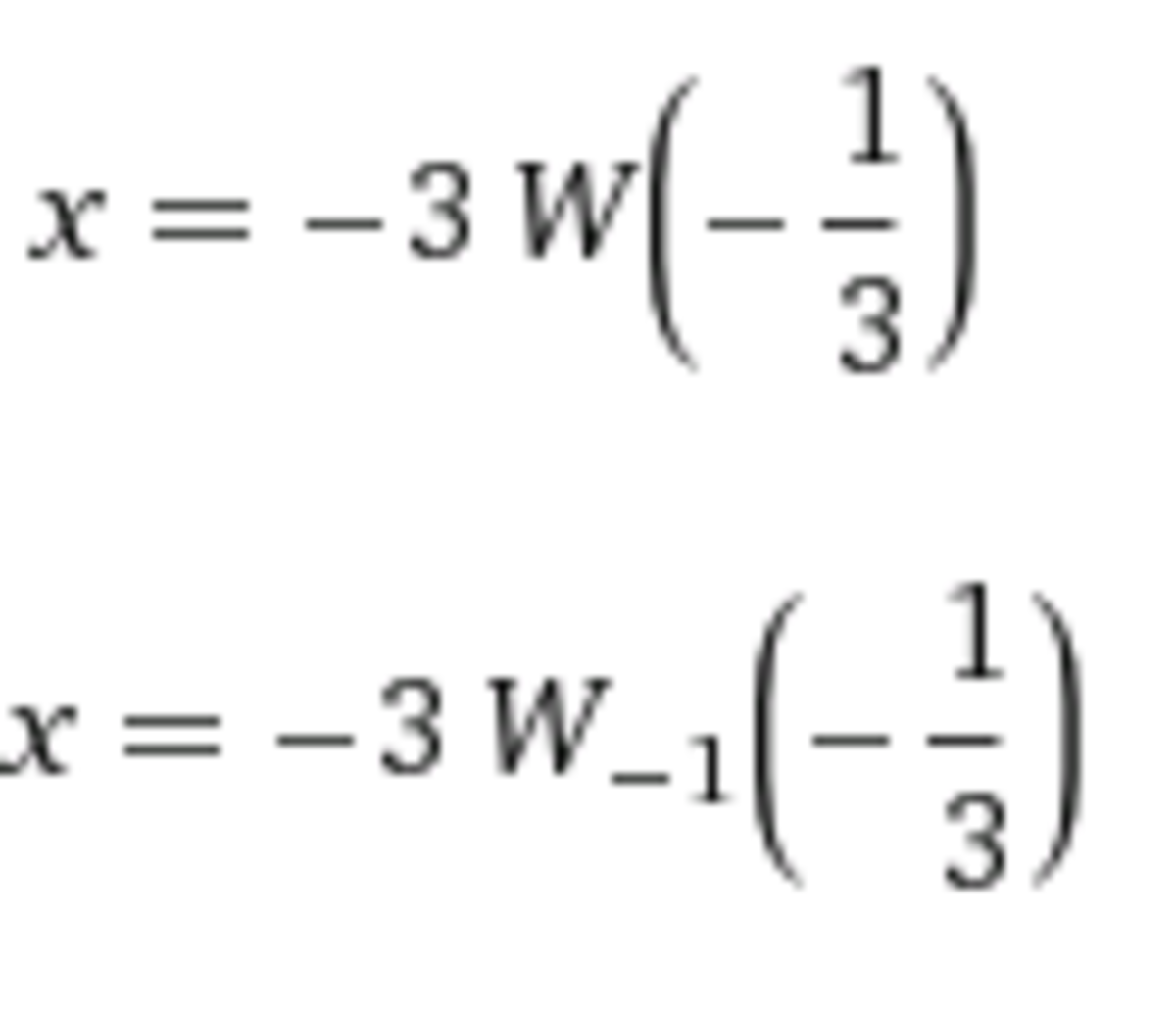
{x == -3 ProductLog[-1/3]} and {x == -3 ProductLog[-1, -1/3]}