Number of triangles
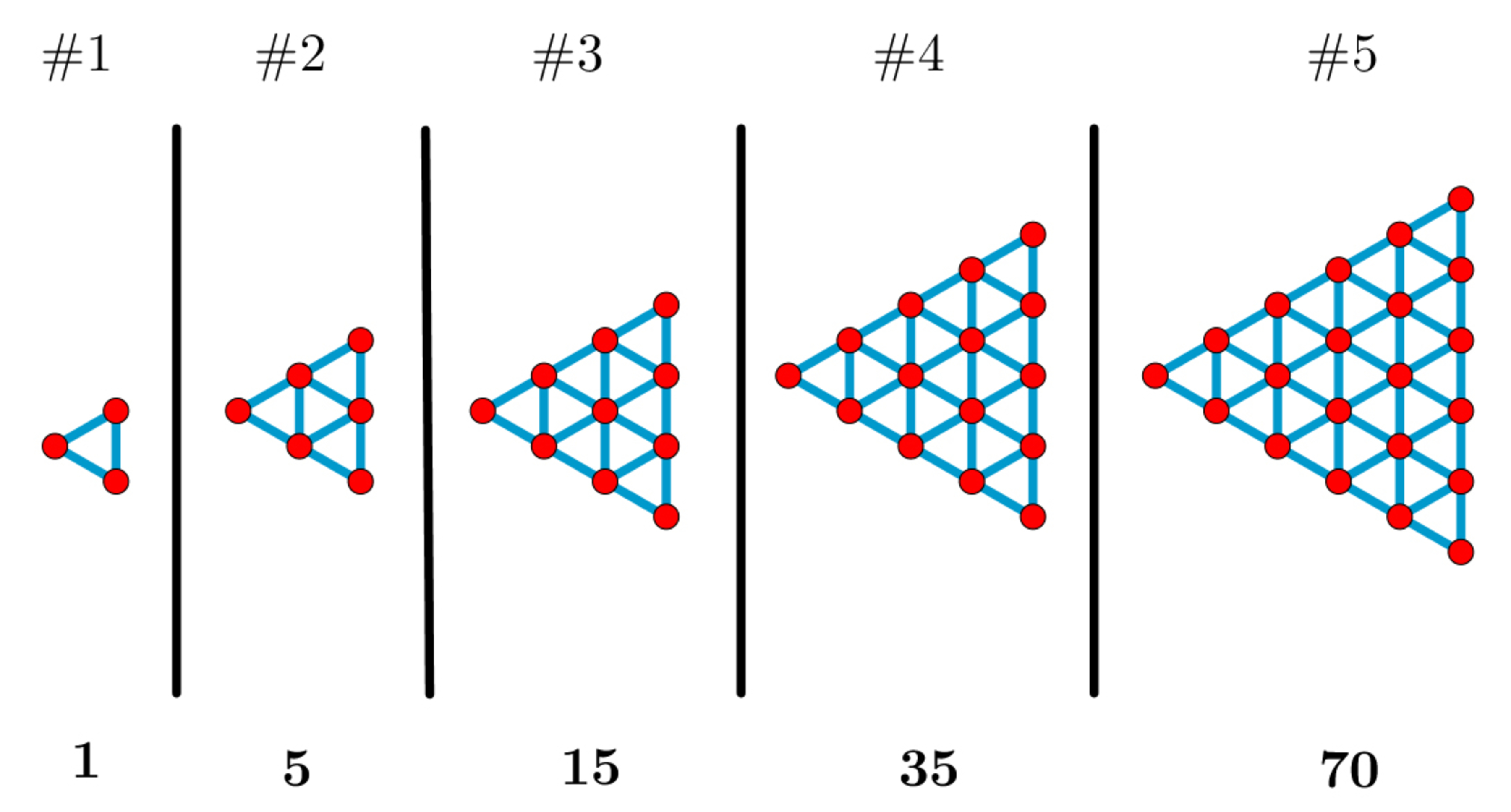
The pattern above: the number of equilateral triangles, the vertices of which are from the red points.
What comes next?
Bonus question:
Generalize for # n .
The answer is 126.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I don't know why this pattern works:
1 5 1 5 3 5 7 0 1 2 6 4 1 0 2 0 3 5 5 6 6 1 0 1 5 2 1 4 5 6 1 1
(Each lowest number is 1 and the number above any two is the sum of them.)
nice solution(+1)
What we are dealing with here are pentatope numbers which are the sum of n tetrahedral numbers. The nth tetrahedral number is in turn the sum of the first n triangular numbers.
A pentatope number is a number in the fifth cell of any row of Pascal's triangle starting with the 5-term row 1 4 6 4 1 either from left to right or from right to left.
The first few numbers of this kind are :
1, 5, 15, 35, 70, 126, 210, 330, 495, 715, 1001, 1365 A pentatope with side length 5 contains 70 3-spheres. Each layer represents one of the first five tetrahedral numbers.
The nth number in the above sequence has the formula C(n + 3, 4)