Number of triangles in 4D cube

Probability Level 3

What is the number of all triangles whose vertices are all on the same face of a 4D cube?

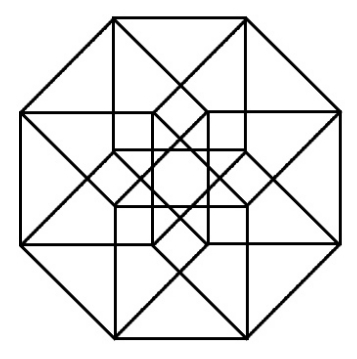
128 64 32 56 96

1 solution

Zico Quintina
May 7, 2018

A 4-D hypercube will have $2^4$ vertices; in 4-D, each vertex will connect $4$ edges. Every pair of edges connecting to a vertex determines a face, so there are $\binom{4}{2}$ faces that meet at each vertex. But each face will be counted four times, once for each of its four vertices, so we have to divide by $4$ . The number of faces is $\dfrac{2^4 \cdot \binom{4}{2}}{4} = \dfrac{16 \times 6}{4} = \boxed{24}$

Draw 2 3D (congruent) cube,and connect their vertices(not all of them,just one vertice to one,so there will only be 8 lines connecting the two cubes) together will form a 4D hypercube.The 2 cubes have 12 faces,and while connecting the vertices,the edges of the 2 cubes will form faces,too.A cube has 12 edges,so there will be 12 faces between the cubes.Last,there are totally 12+12=24 faces.

X X - 3 years, 1 month ago

Right! When I first tried this question, I approached it the same way you did but got stuck on counting the extra faces. Thinking on it some more now, it seems clear that, like you said, each "old" edge would gain one additional face; or alternatively, each "new" edge would connect to three new faces, for $\frac{8 \times 3}{2}=12$ new faces. Thanks for pointing it out.

zico quintina - 3 years, 1 month ago

Number of triangles in 4D cube

1 solution

0 pending reports