Number Pad Snake
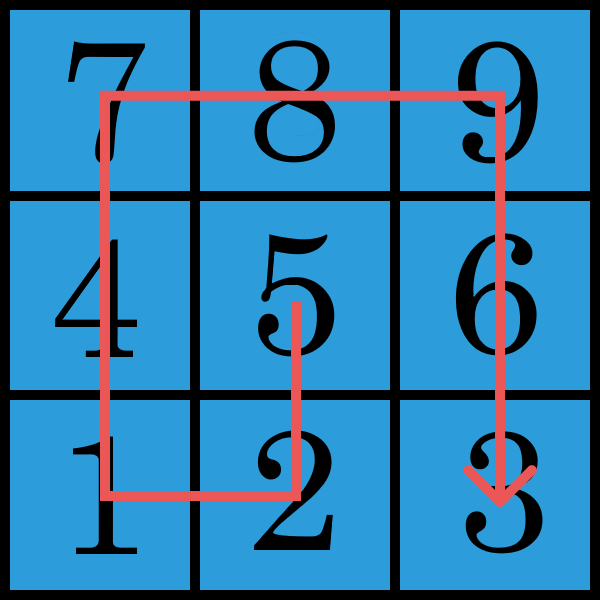
On this number pad , a nine-digit number is made by walking through each digit once, starting from a random digit and only moving to adjacent digits .
That number is then divided by its first digit . In this example, 9 8 7 4 5 6 3 2 1 ÷ 9 = 1 0 9 7 1 7 3 6 9 . Will this method always result in an integer?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
26 solutions
For a rigorous proof you do need to demonstrate that it is possible, following the rules, to create a nine digit number beginning with 5.
My first attempt at a similar proof was to start with the digit 2 and end on an odd number digit. However this argument was flawed because it is impossible to generate a nine-digit number from the grid if you begin in box 2, 4, 6 or 8. (For proof of this impossibility, colour the boxes like a chess board; the path takes you through alternating colours so must begin in the centre or in a corner.)
Log in to reply
Updated the solution with detailed information and required analysis. Please check and give your suggestion.
What happens when you start with 7? I know that it doesn't matter, but is it that it is always, sometimes or never divisible? Trying the numbers 785412369 and 789654123 reveal sometimes but I'm not sure why
maybe there is no apparent rule for 7
Log in to reply
Check the rule in the reference wiki page. https://brilliant.org/wiki/divisibility-rules/
Sir i cant understand Acc to div. Rule by 9 the sum of digits of a number should be divisible by as as the sum always remain 45 every number should be divisible by 9
Log in to reply
Check the wiki link:
https://brilliant.org/wiki/divisibility-rules/
A positive integer 'N' is divisible by 9, if the sum of digits of 'N' is a multiple of 9;
Nine digit number with any combination from 1 to 9 is divisible by 9.(since sum of digits is 45)
My number started with a 4 and ended with an odd one so that is my way
Relevant wiki: Divisibility Rules (2,3,5,7,11,13,17,19,...)
You can start with the number
5
in the middle.
 5
2
1
4
7
8
9
6
3
÷
5
=
1
0
4
2
9
5
7
9
2
.
6
5
2
1
4
7
8
9
6
3
÷
5
=
1
0
4
2
9
5
7
9
2
.
6
The quotient is not an integer.
Nice and unique problem! Try making them a bit harder though, with maybe more restrictions, conditions, etc.
Would the same result occur on a 4x4 grid (base-17)? How about a 5x5 grid? What about an n x n grid in general? What about an a x b grid? A 3-dimensional numberpad? An n -dimensional numberpad? If there's different restrictions on how the number can be formed?
There's a lot of potential in this problem.
I knew going in this problem would be an easy one. In fact I came up with this problem while being bored after a math test. Thanks for the comments and I now might make a much harder part 2.
Log in to reply
I never think to make my problems this easy. This is a nice first basic problem for the week. I'm sure some tough variants await.
To move to a number and then move away from it the number must have 2 available sides. Thus if you start with 2 the sequence must end with either 1 or 3, which means you have an odd number not divisible by 2.
Log in to reply
Actually, you can't make a 9-digit number unless you start with one of the odd numbers.
Interestingly, you can't make a path with 2,4,6 or 8. No matter what number you use is divisible by 1. Any number starting with 3 or 9 will work too, because 1+2+3+4+5+6+7+8+9=45, and 45 divided by 3 =15 and divided by 9= 5. https://brilliant.org/wiki/divisibility-rules/
Actually, you don't have to bother calculating any result at all. If one starts at 5 neither of the numbers will end with a 5....neither with a zero. Hence, there is at least one scenario which violates the condition given in the problem. So the answer is NO. Cheers!
Many starting with 7 are not: Ex: 7 7 8 9 6 5 4 1 2 3 ≈ 1 1 2 8 0 7 7 3 1 . 9
For a number to be completely divisible by 5, it has to end with 5 or 0, which is ENTIRELY NOT POSSIBLE in the given scenario. So the answer is NO.
There is no need to do any test calculations For any chosen route beginning with a 5 the resultant number must end in a 5 or a 0 for there to be an integer result. We have already used the 5 and there is no 0. Therefore the method does not always end in an integer.
Just start moving from five , and move any direction the result wont lead to an integer .
E.g. the number 563214789 is obviously not divisible by 5. Hence the answer must be No.
As others have said, starting at 5 will never produce a multiple of 5, but also if you start at an even digit, then you won't even be able to get to all the digits, because the digits must alternate parity.
You can't start with an even digit because you can't even walk through each digit once that way.
7 7 8 9 6 5 4 1 2 3 = 1 1 2 8 0 7 7 3 1 . 9
Assume that the statement above is true for all cases. Disregarding the first case (the one completed above), the one counterexample that I found is this: 789654123
7 + 8 + 9 + 6 + 5 + 4 + 1 + 2 + 3 = 45 (All the numbers add to 45)
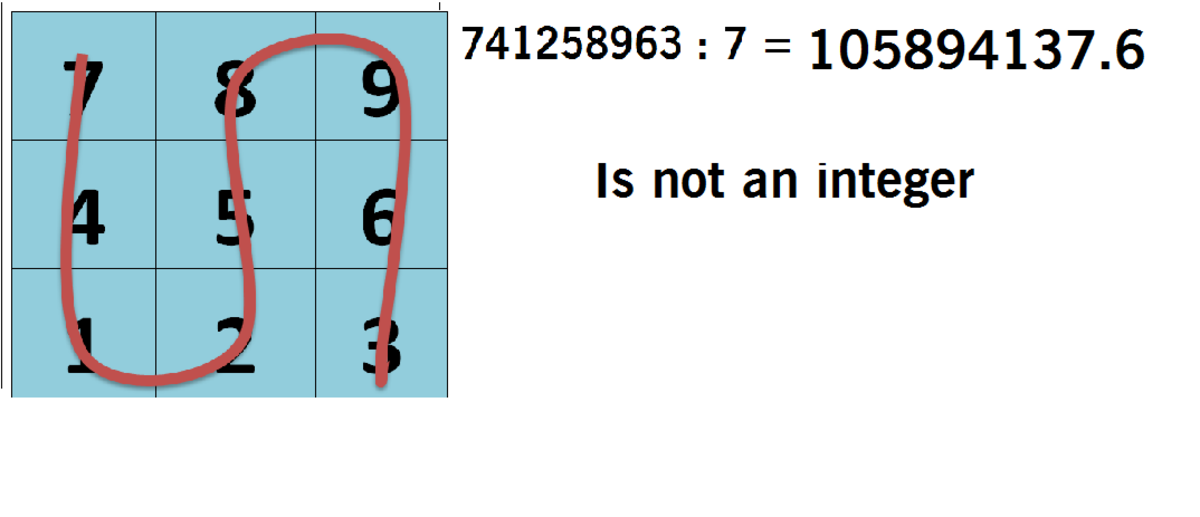
The quotient of 7 4 5 is not an integer.
Contradiction.
Therefore the statement is false .
Really, the number is a counterexample if it starts with 7, regardless of the other numbers in it.
The sum of all the digits is forty five which is not divisible by 6 therefore if you were to start with six you will not end up with an integers |||
For divisibility of a number through 6, the sum of the digits does not need to be divisible by 6, only 3 (It also has to be even).
Log in to reply
That statement contradicts itself
45 is a multiple of 3 but is not even
Log in to reply
the sum of the digits of the number doesn't have to be even, just the number itself
You cannot start with 2, 4, 6 or 8 and make a valid path.
start with 5 and end with a number that's not 5.
Start from 4, you will end up with an odd digit in last.
We cannot start with any even numbers given that you can move only to adjacent ones. We'll end up with an isolated unused number in a corner or center.
A number that is divisible by 5 has to end in a 5 or a 0, and since 0 is not on the number table and 5 can only be used once, if you start with 5 and then divide by 5 at the end, you will not get an integer
If we begin with 5 the number doesn't end in 5 and zero is not given. So the resulting number doesn't end in 5 or zero. So it's not divisible by 5.
Simply start on 5 and take any path through the remaining digits. You can't end on 5 or 0, so the result cannot be divisible by 5.
If you start with 5 the number can't end with 5 and since there's no 0 and any number not ending in a 5 or a 0 is not divisible by 5 no value you make will be divisible by 5.
Answer: No
When a number is made on the number pad, in order for that number to be divisible by the first integer, the last two digits have to divisible by the first integer.
For example, when 7 is used as the first number, the possible numbers are 789654123 and 741258369. The last two digits of both numbers aren't able to be divided equally by 7
(69/7 = 9.8571428571 and 23/7 = 3.2857142857).
Therefore no, the method proposed in the question does not always result in an integer.
Easy way to solve this is to note that a number being divisible by 5 ⟺ last digit is 0 or 5 . Therefore we start with 5 in the middle and any number we make doesn't end with either 0 or 5 and so won't be divisible by 5 .
First, the problem is wrong. You cannot go through all the digits if you start from one of the even numbers.
Second, you have no solution if you start from 5. For a number to be divisible by 5 it must end in 0 or 5. You don't have 0 on the number pad and you just started with 5 so you can't also end with it.
21 is not divisible by 2 if ignore the other digits or else go around via any of the other digits back to 1 since the last digit 1 divided by a 2 is 1/2 i.e. 0.5 which is not an integer. This is the simplest proof aside from start the with and divide by a 5 one which must end with a 5 or 0.
Begin by a even number and end by a odd number.
The is often divisible by 9.
If you start on 5, you cannot possibly achieve an integer division. All numbers divisible by 5 end in 0 or 5. This number pad has no 0, and starting on 5 removes it as a possible final digit.
Relevant wiki: Divisibility Rules (2,3,5,7,11,13,17,19,...)
Answer: No. ( Without Calculation we can derive the result using divisibility test )
The given number pad has digits from 1 to 9. Clearly, it has 5 odd digits and 4 even digits. The adjacent to even digits are odd & adjacent to odd digits are even. The valid moves are odd to even (or) even to odd. If it start with even digit then it is not possible to end with even digit(since number pad has only 4 even digits). So it must start with odd digit, and the generated number will end with odd digit.
The possible start digits are 1, 3, 5, 7, or 9. Suppose, it start with 1, 3 or 9 then the generated number is divisible by 1, 3 or 9 respectively. Since all intigers divisible by 1 and sum of digits 1+2+3+…+9 is 45, which is divisible by 3 and 9. The other two possible start digits are 5 or 7. If it start with 5 then the generated number not divisible by 5. Because it is not possible to get the end digit as 0 or 5. Hence the result always not an integer.