Number Pyramids and Parity
Number Theory
Level
3
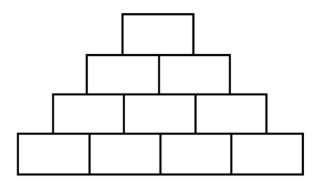
In the number pyramid shown, where all numbers are positive integers, each number is the sum of the two numbers below it.
What is the maximum number of odd numbers that can be in the pyramid?
5
6
7
8
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If any row contained only odd numbers, then all the numbers above that row would have to be even; so to maximize the number of odd numbers, at least one number in each of the bottom two rows would have to be even. Also, in the top two rows at least one of the three numbers will be even. This means at least three numbers in the pyramid will be even, so the maximum number of odd numbers will be 7
Here's an example to show 7 is possible: