Number theory
Number Theory
Level
2
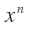 Total number of factors of any perfect square number is always
Total number of factors of any perfect square number is always
Odd or Even depending on the number
None of these
Cannot be determined
Odd
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let S be a perfect square.
We can express S as
S = p 1 x 1 p 2 x 2 p 3 x 3 . . .
Where p 1 , p 2 , etc are prime numbers .
∀ x ∈ { x 1 , x 2 , x 3 , . . . } , 2 ∣ x
The number of divisors is given by i = 1 ∏ n ( x i + 1 )
As all factors are odd numbers, the product will be odd.
As the product is the number of divisors, the number of divisors is odd. ■
"My first attempt at a mildly decent proof."