Number Theory + Co-ordinate Geometry = Challenging problems

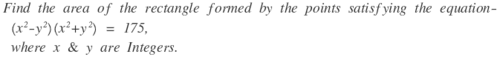
Given $(x^{2} - y^{2})(x^{2} + y^{2}) = 175$ where, x & y are integers.

If x & y are integers each of the two terms on LHS are numbers. This implies RHS = 175 must be product of two numbers. This in turn implies we need to break it up into factors.

175 = 1 x 175 or 5 x 35 or 7 x 25

We further note that some of the two terms on LHS = $2x^{2}$ . This implies (sum of the two factors of 175)/2 must be a perfect square. This happens only with (7, 25).

Hence $x^{2} = (7+25)/2 = 16$ . This gives x = +4 or -4. Similarly one can obtain y = +3 or -3.

So, the rectangle formed has sides (4 - (-4)) = 8 and (3 - (-3)) = 6. Area = 8 x 6 = 48 sq unit.

The first step is to prime factorize 175 to 5,5,7.

We see that $x^2-y^2<x^2+y^2$ .

Thus $x^2-y^2=(5,7)$

We observe that 35 cant be written as the sum of two squares. Thus $x^2+y^2=25$ . The only two integers that satisfy this are (x,y)=(4,3).

Finally, because the equation is centered at (0,0) the question asks us to find $4xy=4(4)(3)=\boxed{48}$ .