Let's Make Digits Distinct!
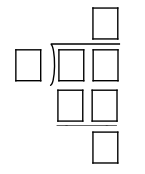
The above shows a long division, where the divisor is strictly greater than the remainder and the quotient is a single-digit number.
Is it possible to fill each box with a distinct, non-negative single digit?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Suppose that there are some digits that work for the given cryptarithm. Let A , B , C , D , E , F , G be distinct nonnegative digits, such that A × B C D + G = C D = E F where E F is the number being divided by A , and G is the remainder. Since E F and C D both have different digits, then E = C + 1 , so C D + G 1 0 C + D + G 1 0 C + D + G D + G D = E F = 1 0 E + F = 1 0 C + 1 0 + F = 1 0 + F = 1 0 + F − G where F < G , so D < 1 0 . However, A × B = C D = 1 0 C + D = 1 0 C + 1 0 + F − G = 1 0 ( C + 1 ) + ( F − G ) = 1 0 E + ( F − G ) Contradiction: This can't happen since F − G is the negative ones digit, and since C = E violates the assumption that all digits are different.
Thus, it is impossible to fill all boxes with distinct digits.