Number Theory Intermediate Challenges-I

Number Theory Level 4

Cozy the Cat and Dash the Dog are going up a staircase with a certain number of steps. However, instead of walking up the steps one at a time, both Cozy and Dash jump. Cozy goes two steps up with each jump (though if necessary, he will just jump the last step). Dash goes five steps up with each jump (though if necessary, he will just jump the last steps if there are fewer than 5 steps left). Suppose that Dash takes 19 fewer jumps than Cozy to reach the top of the staircase. Let $s$ denote the sum of all possible numbers of steps this staircase can have. What is the sum of the digits of $s$ ?

This problem is from the AMC.This problem is part of this set .

The answer is 13.

2 solutions

Kevin Hong
Mar 29, 2015

Concepts involved: Step Function (no pun intended) and Pattern Recognition.

We first set variables for Cozy and Dash. They will be 2(x+19) and 5x respectively. The number of steps in the staircase will be y.

Thus we get the equation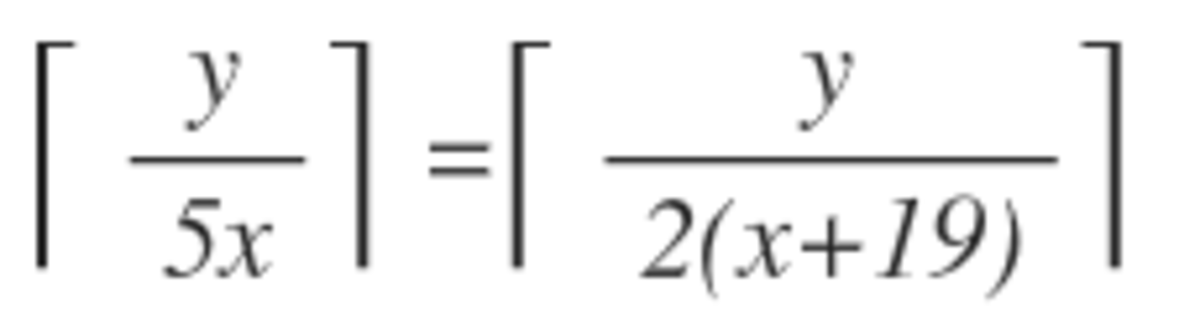

We can solve this algebraically and get a solution of 12.66666... This number is a good indicator of around where x can be. Next a little simple arithmetic is required as we multiply 12.66 plus or minus 1 by 5. This gets a high and low of 69 and 63 respectively.

Next we plug and chug dividing all numbers from 63-69 by 2 and 5. If there is a decimal in place we round up.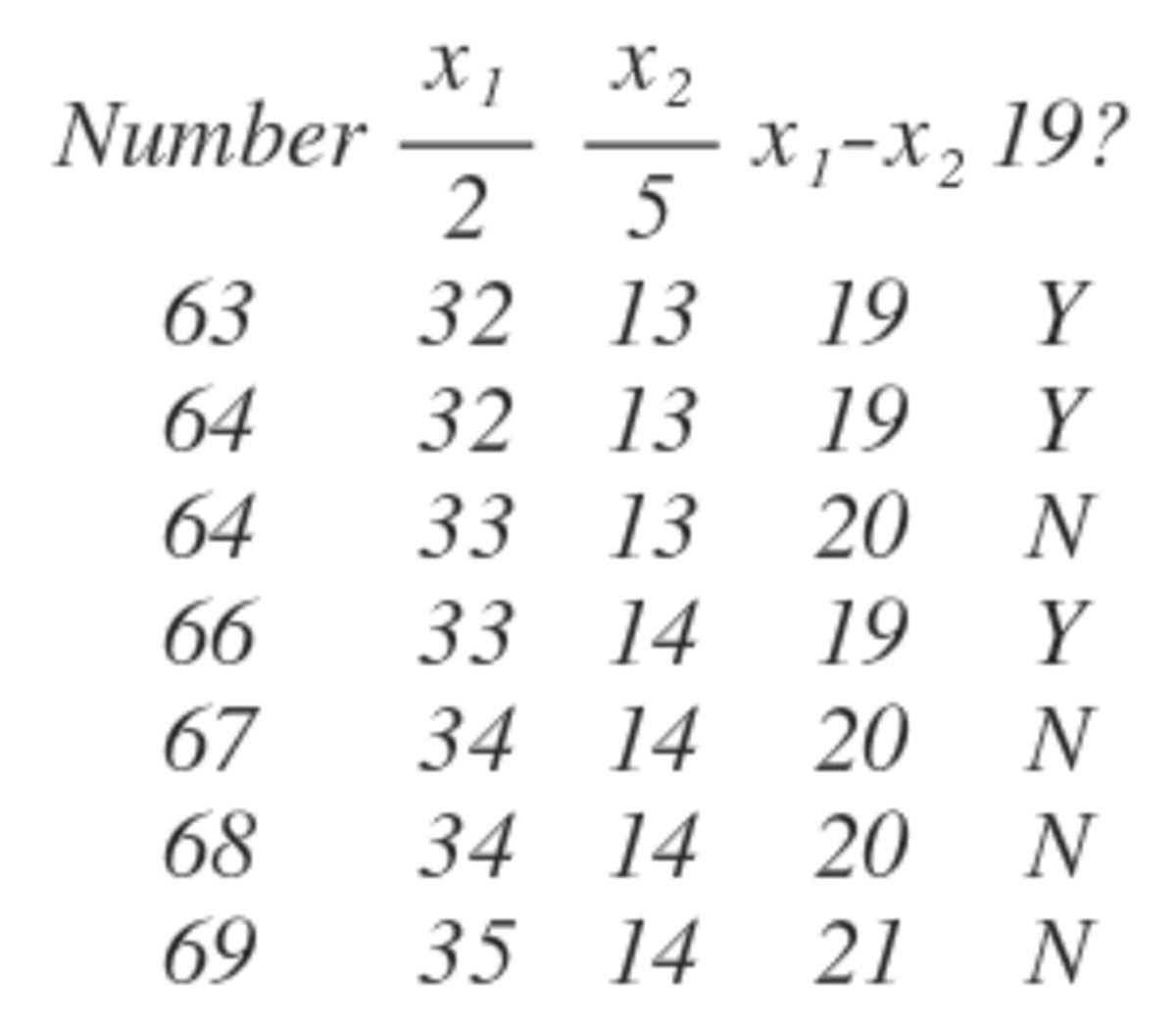

Finally we see that 63,64 and 66 work. Their sum is 193. The sum of the digits of 193 is 13, our answer.

A few things to note:

1.) Plus or minus 1 was chosen as it works out with the step function. This allows the "middle" number to have its surroundings checked. In other words a step function is given one value for a range of 1.

2.) I really doubt that "plugging and chugging" is the fastest method to work it out from there. But it did take longer for me to type this all out than to do the problem. If anyone knows some shortcuts please do share! Step functions are really lacking on the internet.

I noticed 63 and 64 were possibilities, and that 65 didn't work. So I added them up and was shocked when the answer wasn't 10. I thought there must've been a problem with the problem, so I was wondering if the stairs were counted funny. So I tried 62 and 63 as well as 64 and 65 and that used up my 3 tries. It never crossed my mind that 66 could be an option after I saw 65 didn't work. I think I learned a lot from the problem. I did get the answer of 63 and 64 rather quickly though. I noticed since 2 x 5 is 10, that every 10 steps, they will land on the same step. Thus for every 10 steps, since it takes the dog 2 jumps and the cat 5 jumps, we know that the cat will be 3 jumps behind every 10 steps. Since we care about when the cat is exactly 19 jumps behind, we do 19/3 and we wind-up with 6.33333333333... So we know that we can fast-forward to the 6th flight of 10 steps. Both the dog and cat are now standing on the 60th stair. To get to the 60th stair, it took the dog 12 jumps and the cat 30 jumps. Since 30-12 is 18, we know that a few more steps need to be climbed to see them 19 jumps apart. The dog will jump to the 65th step on his 13th jump. So the cat needs to make two jumps for the cat and dog to be 19 jumps apart. Thus we know 63 and 64 are options for the number of stairs. What didn't cross my mind, though, is that the dog can leap again and the cat can leap again. Thus if we add one more stair, making the dog have to leap again for 1 stair, there would be 66 stairs. And the cat would get there 19 jumps behind. Thus 63. 64, and 66 are the possible numbers of stairs. Add them up, and "s" is 193. 1+9+3 is 13, our final answer.

Menachem Avinoam - 5 years, 6 months ago

74;67 are satisfying

Sudhamsh Suraj - 4 years, 3 months ago

Niranjan Khanderia
Oct 19, 2017

Let Dash jumps ' n ' times and last k steps. Then Dash cover 5n 0r 5n+k steps.
So for 5n of Dash, Cozy covers (a) 2(n+19)=2n+38 0r (b) 2(n+18) +1=2n+37 steps;
And 5n+k of Dash. Cozy covers (c) 2(n+1+19)=2n+40 0r (d) 2(n+18) +1=2n+37 steps;
Since they cover the same number of steps.
So (a) 5n=2n+38... OR ...(b) 5n=2n+37... OR ...(c) 5n+k=2n+40... OR ...(d) 5n+k=2n+39 both n and k are integers. k = 1, 2, 3, 4.
So (a) 3n=38 ... Or ... (b) 3n=37 ... Or ... (c) 3n=40 - k... Or ... (d) 3n=39 - k
(a) That is 38=3n ... and ... (b) 3n=37 ............both not possible.
(c) That is 40-k=3n, ..........(i) so n=13, ... for...k=1.....Total steps=S1=5 * 13+1= $\color{#D61F06}{66}.\\$
...........So.........................(ii) so n=12, ... for...k=4.....Total steps=S2=5 * 13+4 = $\color{#D61F06}{64}.\\$
(d) That is 39-k=3n, so n=12, ... for...k=3......Total steps=S3=5 * 12+3= $\color{#D61F06}{63}. \\$
s=S1+S2+S3=193..........1+9+3=13.
Since k=1, 2, 3, 4 no other solution possible.

Number Theory Intermediate Challenges-I

The answer is 13.

2 solutions

0 pending reports