Factorials are large.
Is the following summation larger than 4?
2 ! 1 ! + 3 ! 2 ! + 4 ! 3 ! + … + 1 0 0 ! 9 9 !
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Discussions for this problem are now closed
Please explain little more about the formula used ,thanks.
H n = 1 1 + 2 1 + 3 1 + … + n − 1 1 + n 1 can be approximated by γ + ln n .
It turns out that γ = ∫ 1 ∞ ⌊ x ⌋ 1 − x 1 d x as well, along with satisdying other interesting equations like γ = − Γ ′ ( 1 ) = k = 1 ∑ ∞ ( ⌊ k ⌋ 2 1 − k 1 − k 2 1 ) .
Wouldn't it be ln(n+1) - 1 (for the additional 1 added to make the series 1/n) and hence equal to 4.62-1 = 3.62?
You forget that I've added the constant γ .
I was thinking to make this an approximation to the integration of 1/x That answer yields 3.91 Seems that it is not that accurate
This is because you are taking I = ∫ 2 1 0 0 x d x rather than I ′ = ∫ 1 1 0 0 x d x , which is a careless mistake.
Reviewing the definition of Riemann sums will tell you why I ′ is more accurate than I .
The series is equivalent to 2 1 + 3 1 + 4 1 + . . . + 1 0 0 1
Let S be the sum S > 4 3 + 8 4 + 1 2 4 + . . . + 1 0 0 4
S > 4 3 + 4 ( 2 1 + 3 1 + 4 1 + . . . + 2 5 1 )
but ( 2 1 + 3 1 + 4 1 + . . . + 2 5 1 ) > 2 4 × 2 5 1
S > 4 3 + 4 ( 2 5 2 4 )
S > 1 0 0 4 5 9 which is greater than 4
Moderator note:
This solution has been marked wrong 2 1 > 4 3 , so your second line is wrong.
Can you help me figure out why this approximation exceeds the asymptotic limit.
I don't know how you derived the formula in the second line, however look at the 3rd line, on the RHS you have:
4 ( 2 1 + 3 1 + … 2 5 1 ) ≥ ( 2 1 + + 3 1 + … 9 6 1 ) and also
4 3 ≥ 2 1 + 9 7 1 + 9 8 1 + 9 9 1 + 1 0 0 1
therefore you have to reverse the inequality sign
Moderator note:
This solution has been marked incomplete because it fails to show the most crucial step.
Moderator note:
This solution has been marked wrong for obvious reasons. The summation clearly shows that it is the sum of squares of whole numbers, while the sum in question is actually the sum in reciprocal of whole numbers. Furthermore, the use of computational aid in not required in this question.
Are you sure?
that is not like that?
1 2 3 4 5 6 |
|
frac(1, n) is good enough :)
ahh Python, very clever
I think the range should be xrange(1,99)
Not quite, xrange(1, 99) would output the result of the following:
1!÷2! + 2!÷3! ... 98!÷99! ≈ 4.177
This is because the parameters for the generator function xrange are start and stop . Start is the first number that xrange will output and stop is the number at which the generator function halts. The xrange function will never output stop .
I always thought that was weird, too, but just remember to make stop equal to 1 more than the number you want to end on.
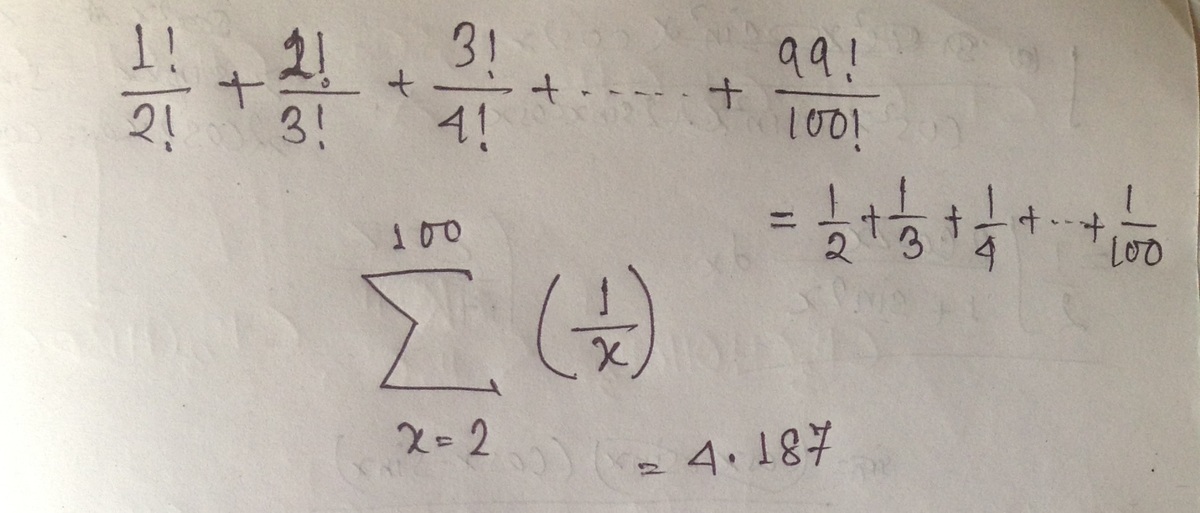
First, we simplify each term. It is easy to see that n ! ( n − 1 ) ! = n 1 , and so the sum becomes S = 2 1 + 3 1 + … + 1 0 0 1 .
This is one less than the 100th harmonic number H n , which can be approximated by the asymptotic limit γ + ln n where γ is the Euler-Mascheroni constant . Taking n = 1 0 0 and subtracting one gives
S ≈ γ + ln 1 0 0 − 1 ≈ 4 . 1 8 2 > 4