Numbers in a pyramid
In the circle puzzle below, dashed red arrows mean to add and solid blue arrows mean to multiply.
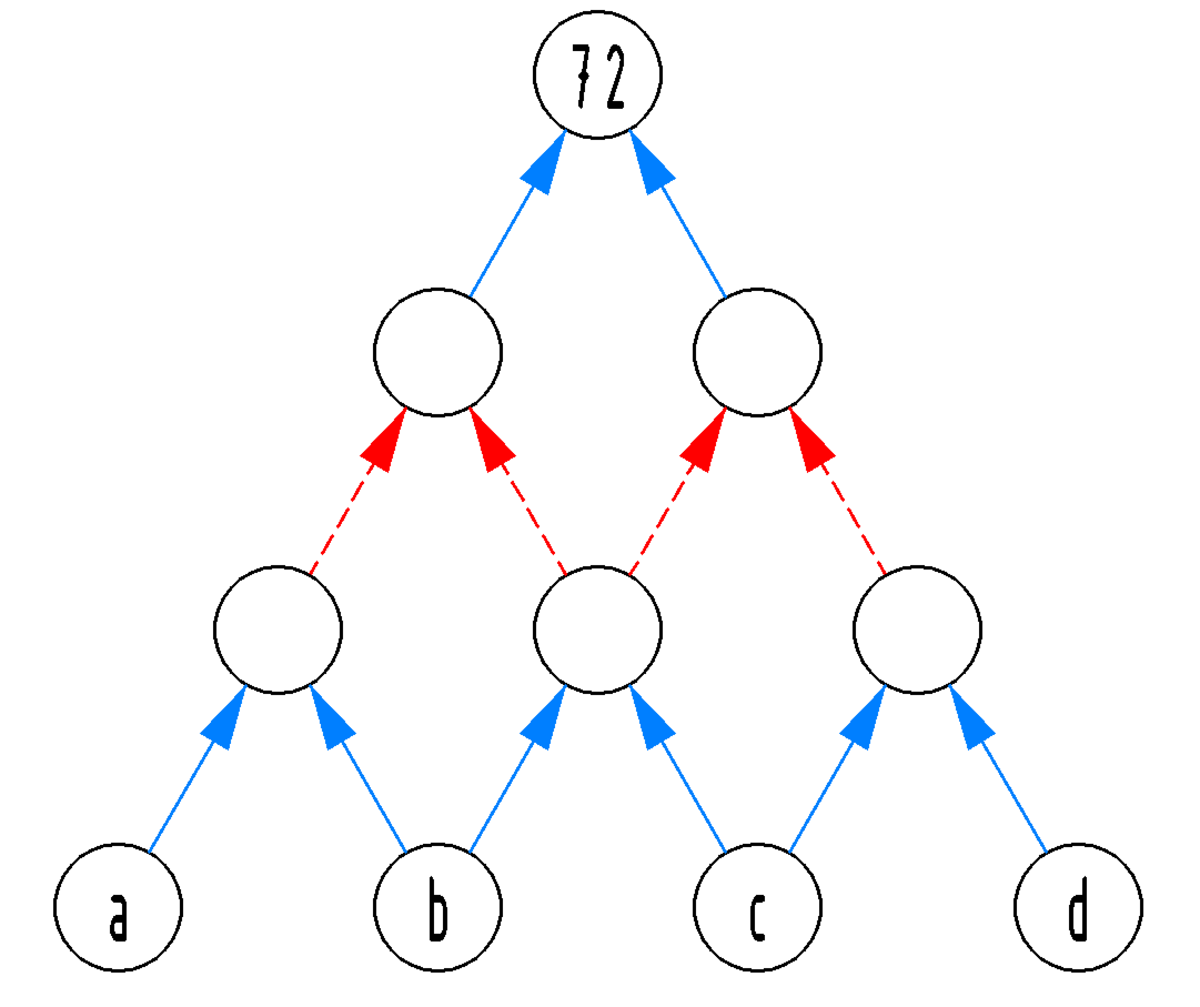 If the letters
a
,
b
,
c
and
d
each represent a different single-digit positive integer and
a
<
d
and
b
<
c
then what is the value of the 4-digit integer
a
b
c
d
?
If the letters
a
,
b
,
c
and
d
each represent a different single-digit positive integer and
a
<
d
and
b
<
c
then what is the value of the 4-digit integer
a
b
c
d
?
For instance: if a = 1 , b = 2 , c = 3 and d = 4 then a b c d = 1 2 3 4 .
The answer is 4125.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Following the rules of the puzzle, the numbers in two circles on the second row can be expressed respectively as a b + b c and b c + c d , so that
( a b + b c ) ( b c + c d ) = b c ( a + c ) ( b + d ) = 7 2
Since a < d and b < c , let c = b + m and d = a + n , such that a , b , m , n are all positive integers. Then, let x a , x b , x m , x n denote possible nonnegative integers, ranging from 0 to 8 , such that a = x a + 1 , b = x b + 1 , c = x b + x m + 2 and d = x a + x n + 2 . Substituting, we have
( x b + 1 ) ( x b + x m + 2 ) ( x a + x b + x m + 3 ) ( x a + x b + x n + 3 ) = 7 2
If b is even, then x b = 2 k − 1 for positive integer k , which simplifies the expression to
2 k ( x m + 2 k + 1 ) ( x a + x m + 2 k + 2 ) ( x a + x n + 2 k + 2 ) = 7 2
But if k = 1 , then 2 k ⋅ ( 2 k + 1 ) ⋅ ( 2 k + 2 ) 2 = 9 6 > 7 2 , which shows that the equation above does not have a solution of nonnegative integers. So since 2 k is strictly increasing, it suffices to check the possible cases for b = x b + 1 = 1 , where the equation to look at is
( x m + 2 ) ( x a + x m + 3 ) ( x a + x n + 3 ) = 7 2
Either ( x m + 2 ) is even or odd. As the prime factorization of 7 2 is 2 3 ⋅ 3 2 ,
Odd Cases: If ( x m + 2 ) is odd, the possible value of c is either 3 ( x m = 1 ) or 9 ( x m = 7 ). As each of the factors is strictly increasing, ( x a + x m + 3 ) is greater than ( x m + 2 ) , which shows there is no possible solution for x m = 7 . For x m = 1 , we have
3 ( x a + 4 ) ( x a + x n + 3 ) = 7 2 ⟹ ( x a + 4 ) ( x a + x n + 3 ) = 2 4
which implies that the possible factorization of 2 4 is 4 ⋅ 6 . That simplifies to x a = 0 and x n = 3 . However, a = b = 1 , which violates the condition that a , b , c and d are distinct.
Even Cases: Otherwise, if c is even, let x m = 2 ℓ , where ℓ is a nonnegative integer. Then, the equation to look at is
( 2 ℓ + 2 ) ( x a + 2 ℓ + 3 ) ( x a + x n + 3 ) = 7 2 ⟹ ( ℓ + 1 ) ( x a + 2 ℓ + 3 ) ( x a + x n + 3 ) = 3 6
Following what we learned about the solutions for even values of b , the necessary condition for finding the possible values is 3 ( ℓ + 1 ) ( 2 ℓ + 3 ) ≤ 3 6 , which solves to 4 1 ( − 5 − 9 7 ) ≤ ℓ ≤ 4 1 ( 9 7 − 5 ) . As we are interested in nonnegative solutions, the values of ℓ to check are 0 and 1 as 1 < 4 1 ( 9 7 − 5 ) < 2 .
If ℓ = 1 , then ( x a + 5 ) ( x a + x n + 3 ) = 1 8 (from ( ℓ + 1 ) = 2 ). As no possible factorization of 1 8 , involving only two integers, exists, no solution exists.
Otherwise, ℓ = 0 , where ( x a + 3 ) ( x a + x n + 3 ) = 3 6 . As the possible factorizations of 3 6 are 4 ⋅ 9 and 6 ⋅ 6 , the possible solutions of ( x a , x n ) are ( 1 , 5 ) (for 4 ⋅ 9 ) and ( 3 , 0 ) (for 6 ⋅ 6 ). Checking, we see that the only existing solution is ( 3 , 0 ) , where a = 4 , b = 1 , c = 2 , d = 5 as ( 1 , 5 ) yields a = c = 2 .
Ground Level circles : a , b , c , d
First Floor circles (X) : ab , bc , cd
Second Floor circles (+) : b(a + c) , c(b + d)
Top Level circle (X) : 72 = bc(a + c)(b + d)
We were told that a ≠ b ≠ c ≠ d & 0 < a, b, c, d < 10 , so we try factoring 72 into 4 factors, with the smallest 2 being NOT equal.
72
= 1 X 2 X 2 X 18
= 1 X 2 X 3 X 12
= 1 X 2 X 4 X 9
= 1 X 2 X 6 X 6
= 1 X 3 X 3 X 8
= 1 X 3 X 4 X 6
= 2 X 3 X 3 X 4
Since all of the numbers a, b, c & d are positive integers, logically
b < b + d & c < a + c
other than the given
b < c & a < d
Thus, b < c < a + c and also b < b + d simultaneously, making it the littlest of the factors.
72 = 1 X 2 X 2 X 18
18 can only be the sum of two nines if both its summands has to be single digit positive integers, but neither 1 or 2 equal 9
72 = 1 X 2 X 3 X 12
If b = 1, then it can only be that 12 = a + c, and c forced to be 3 and 2 = b + d with b = 1 = d, which is contradictory to the given conditions.
72 = 1 X 2 X 4 X 9
If b = 1, then (c,a,d) = {2, (2,7), (8,3)} for a solution of (b,c,a,d) = {1, 2, 7, 3} , but here a > d and as such is invalid
72 = 1 X 2 X 6 X 6
If b = 1, then we have a solution of (b,c,a,d) = {1, 2, 4, 5} , and here a < d and thus validated
72 = 1 X 3 X 3 X 8
If b = 1, then we have a solution of (b,c,a,d) = {1, 3, 5, 2} , but here a > d and as such is invalid
72 = 1 X 3 X 4 X 6
If b = 1, then (c,a,d) = {(3,4), [(1,3), 2], [(5,3), 2]} for a solution of (b,c,a,d) = {(1, 3, 1, 5), (1, 3, 3, 3), (1, 4, 2, 2)} , but here none of these are completely distinct integers with b = a = 1 or c = a = d = 3 or a = d = 2 respectively and as such are all invalid
72 = 2 X 3 X 3 X 4
If b = 2, then d can only be either 1 or 2, but neither can be right because 0 < a < d and d ≠ b respectively.
Answer : (b,c,a,d) = {1, 2, 4, 5}
Rearranging, we get abcd = 4125
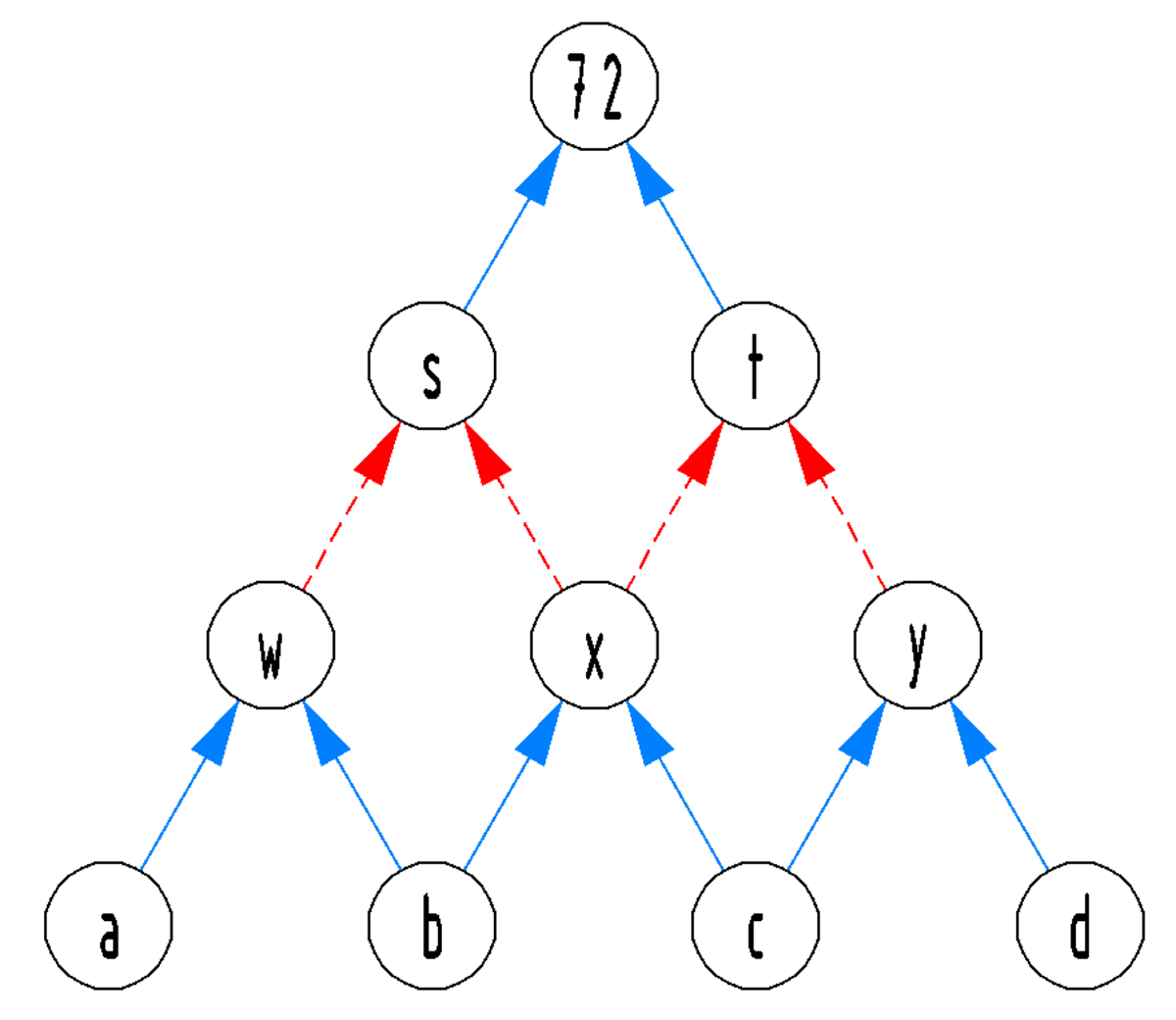
72 factors out as:
1* 72
2* 36
3* 24
4* 18
6* 12
8* 9
Since w=a* b and a≠b≠c≠d (different single digit positive integers) that means w≥2. Same applies to x and y, x=b* c and b≠c and y=c* d and c≠d so x≥2 and y≥2. Now, s=w+x so s≥4 and t=x+y so t≥4.
That means the first three options (1* 72, 2* 36 and 3* 24) don't offer a solution since they all require s<4 or t<4.
To explore the other possibilities we'll simplify the problem a bit by realizing that s and t are interchangeable as are w and y, a and d, and b and c:
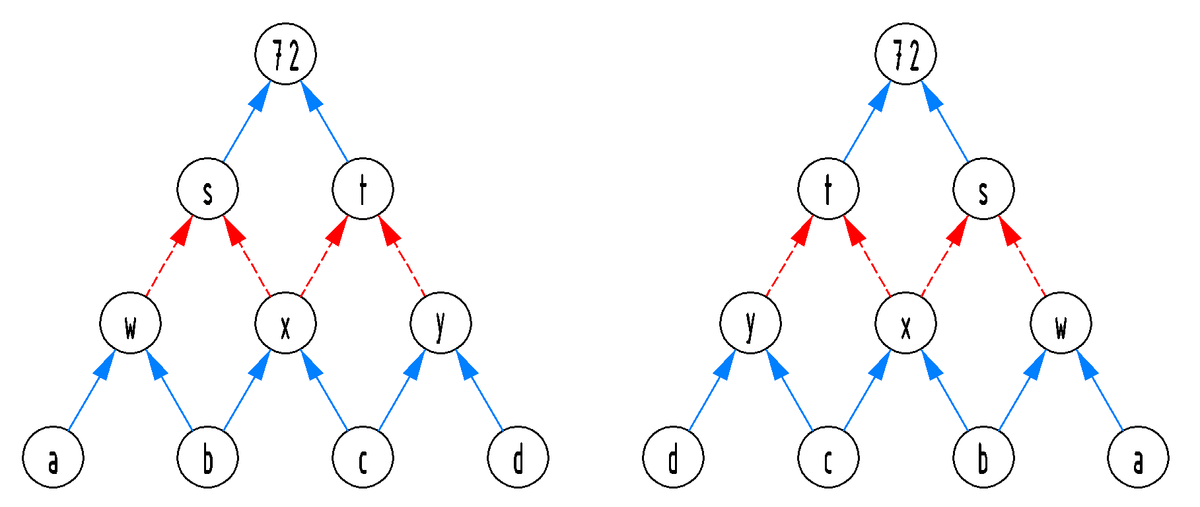 So we'll only explore for s.
So we'll only explore for s.
The next option (4* 18) has s=4. If s=4 then either w=1 and x=3 or w=2 and x=2 or w=3 and x=1. Since w≥2, x≥2 and w≠x this doesn't offer a solution.
With the last option (8* 9) we have s=8. If s=8 then w=2 and x=6 or w=3 and x=5.
If w=2 and x=6 then y=3 (t=9=x+y). If y=3 then c=1 and d=3 or c=3 and d=1. But with w=2 that means a=1 and b=2 or a=2 and b=1. So we'd need c=1 or d=1 and a=1 or b=1 and since a≠b≠c≠d that doesn't offer a solution.
If w=3 and x=5 then y=4 and if y=4 then c=1 and d=4 or c=4 and d=1 (c≠d≠2). But with w=3 that means a=1 and b=3 or a=3 and b=1. So we'd need c=1 or d=1 and a=1 or b=1 and since a≠b≠c≠d that doesn't offer a solution either.
So the option (6* 12) has to be the one to go with, it's the only one left.
Now, If s=6 then w=2 and x=4 or w=4 and x=2 (w≠x≠3 and w≥2).
If w=2 and x=4 then either a=1 and b=2 or a=2 and b=1.
If a=1 and b=2 then c=2 (x=4=b* c) and since b≠c that doesn't offer a solution.
If a=2 and b=1 then c=4. With x=4 and t=12 then y=12-4=8. And if y=8 then d=y/c=8/4=2. But a=2 and since a≠d that doesn't offer a solution either.
If w=4 and x=2 then either a=1 and b=4 or a=4 and b=1.
If a=1 and b=4 then c=1 (x=4=b* c) and since b≠c that doesn't offer a solution.
If a=4 and b=1 then c=2. With x=2 and t=12 then y=12-2=10. And if y=10 then d=y/c=10/2=5.
And there we have the solution a=4, b=1, c=2 and d=5.
Of course with the interchangeability of the letters as mentioned, another solution would be a=5, b=2, c=1 and d=4 but since it is stated that a<d and b<c in this case that isn't a valid solution.
SOLUTION:
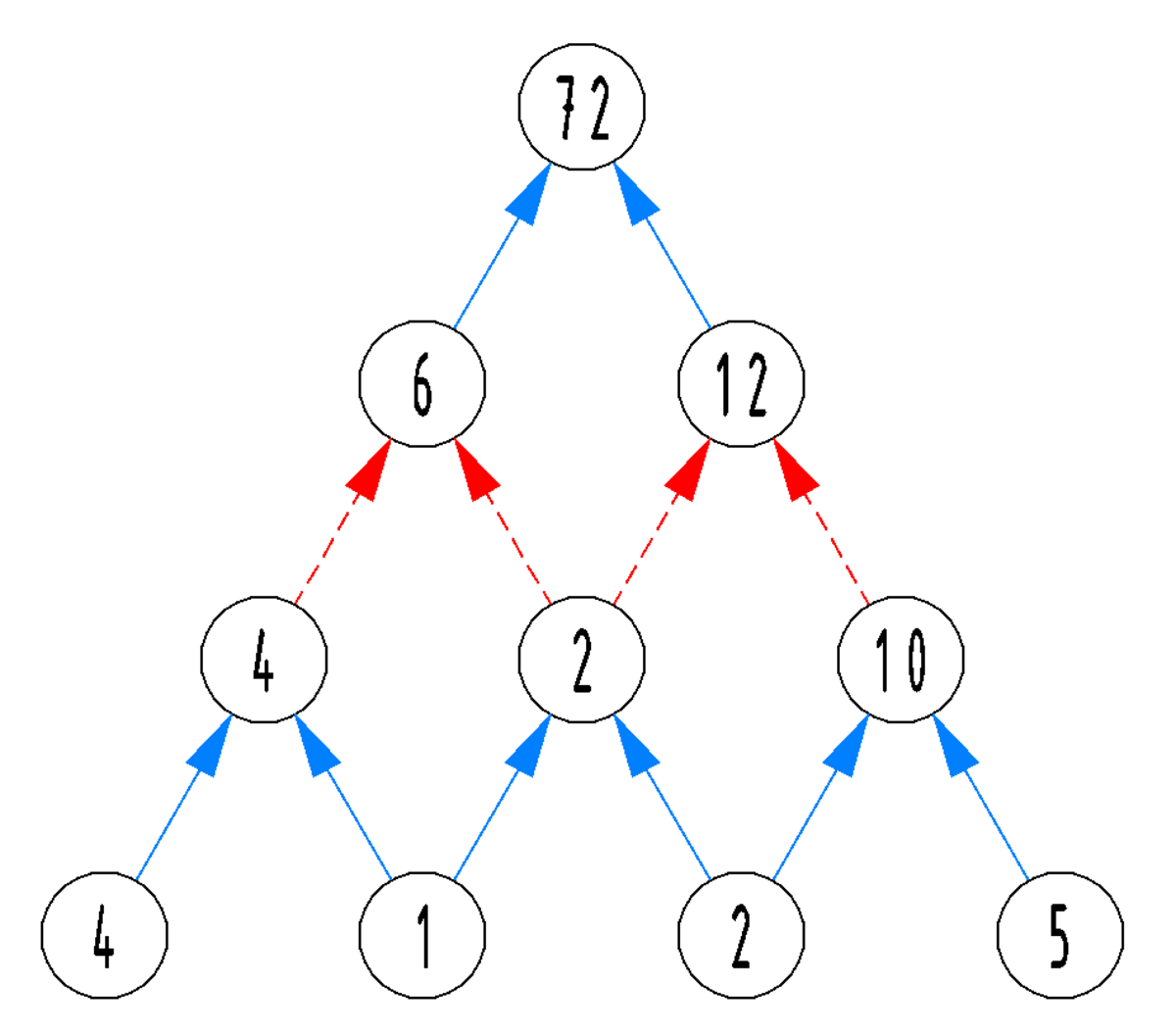
So abcd=4125.
The third row of circles would be a b , b c , and c d , the second row of circles would be a b + b c = b ( a + c ) and b c + c d = c ( b + d ) , and the top circle would be 7 2 = b c ( a + c ) ( b + d ) .
Assume b ≥ 2 . Since c > b then c ≥ 3 , and since d > a then d ≥ 2 , that means b c ( a + c ) ( b + d ) ≥ 2 ⋅ 3 ⋅ ( 1 + 3 ) ⋅ ( 2 + 2 ) = 9 6 . However, 7 2 < 9 6 , so b = 1 .
Assume c ≥ 4 . Since a = b = 1 then a ≥ 2 , and since d > a then d ≥ 3 , that means b c ( a + c ) ( b + d ) ≥ 1 ⋅ 4 ⋅ ( 2 + 4 ) ⋅ ( 1 + 3 ) = 9 6 . However, 7 2 < 9 6 , so c ≤ 3 .
Assume c = 3 . Since a = b = 1 then a ≥ 2 , and since d > a and d = c = 3 then d ≥ 4 , that means b c ( a + c ) ( b + d ) ≥ 1 ⋅ 3 ⋅ ( 2 + 3 ) ⋅ ( 1 + 4 ) = 7 5 . However, 7 2 < 7 5 , so c = 3 .
Since c ≤ 3 and c = 3 and c = b = 1 , it must be that c = 2 .
Assume a = 3 . Then a + c = 3 + 2 = 5 , and b c ( a + c ) ( b + d ) is divisible by 5 . However, 7 2 is not divisible by 5 , so a = 3 .
Assume a ≥ 5 . Since d > a then d ≥ 6 , that means b c ( a + c ) ( b + d ) ≥ 1 ⋅ 2 ⋅ ( 5 + 2 ) ⋅ ( 1 + 6 ) = 9 8 . However, 7 2 < 9 8 , so a ≤ 4 .
Since a ≤ 4 and a = 3 and a = b = 1 and a = c = 2 , it must be that a = 4 .
Solving 7 2 = b c ( a + c ) ( b + d ) with a = 4 , b = 1 , and c = 2 gives d = 5 .
Therefore, the four-digit integer is 4 1 2 5 .