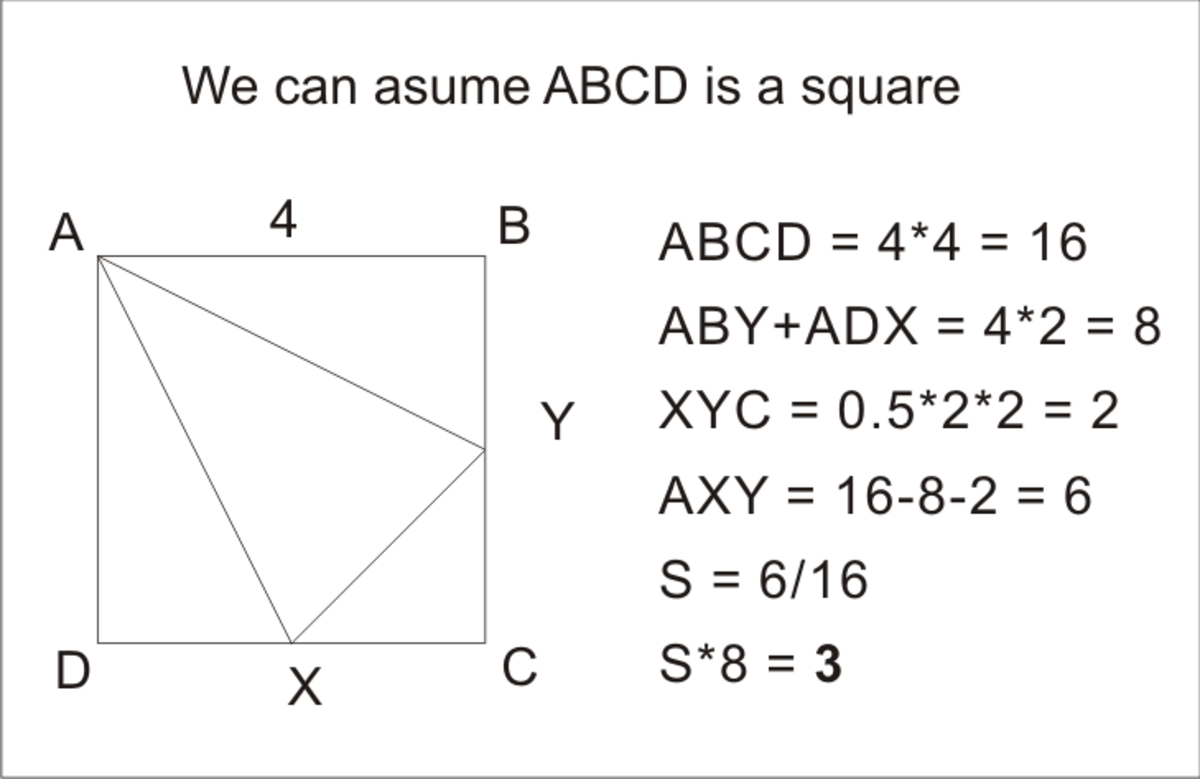
Trapped Triangle
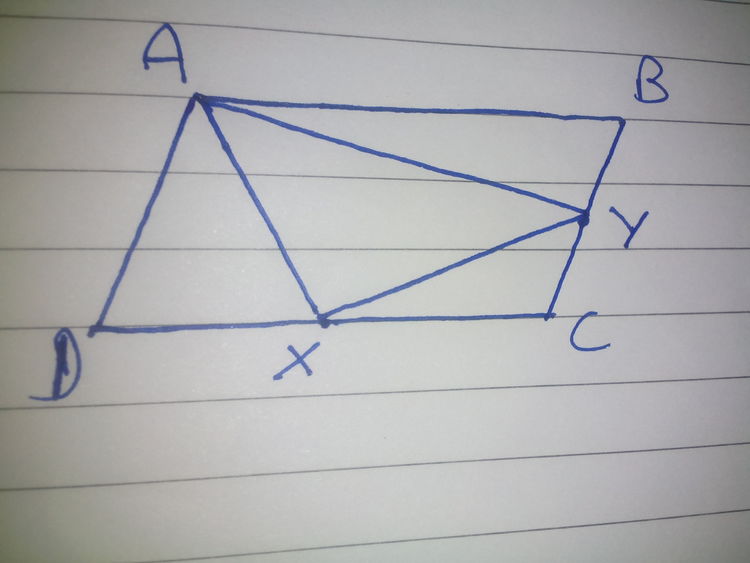 In the above picture, X and Y are midpoints of DC & BC. Area of triangle AXY can be expressed as S times of the area of ABCD. Find S*8.
ABCD is a //gm
In the above picture, X and Y are midpoints of DC & BC. Area of triangle AXY can be expressed as S times of the area of ABCD. Find S*8.
ABCD is a //gm
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Assuming ABCD to be a parallelogram:
-Let U be the midpoint of AB , V the midpoint of AD and O the midpoint of both UX and VY .
-As Y is the midpoint of BC , ABY is 2 1 of ABYV , which is 2 1 of ABCD ., thus ABY is 4 1 of ABCD .
-Similarly as X is the midpoint of AD , ADX is 2 1 of ADXU which is 2 1 of ABCD ., thus ADX is 4 1 of ABCD ..
- CXOY is 4 1 of ABCD . and CXY is 2 1 of this area so CXY is 8 1 of ABCD .
Finally AXY = (1- ( 4 1 + 4 1 + 8 1 )) x ABCD , so S = 8 3
Thus 8 × S =3
AXY =[ 1- (1/4 +1/4 +1/8) ] * ABCD
Let a be the height of ABCD; b be the length CD=AB; ar of ABCD = ab; ar of triangle ADX=ab/4; ar of triangle XCY= ab/8; ar of triangle ABY= ab/4; ar of triangle AXY= Sab=ab-(ab/4)-(ab/8)-(ab/4)=3ab/8; S=3/8;S 8=(3/8) 8=3
If area of //gm is Q, Area of ADX is Q/4. Area of ABY = Q/4. Area of XCY = Q/4. Remaining area = Q-Q/4-Q/4-Q/8=3*Q/8
Area of the given triangle is equal to the area of the parallelogram minus sum of areas of the remaining three triangles. And, two of the triangles share a common base (with the parallelogram) but half the altitude, so their areas are both 1/4 of parallelogram, and the third triangle has both the base and the altitude half of those of parallelogram so its area is 1/8 of that of parallelogram. Therefore, required area = (1-1/4-1/4-1/8)xparallelogram.
Assume the longest side is 4 units and smaller side is 2 units. So area of parallelogram is 8 Sq.units.
X is mid point of larger side, so BX =2, XC=2
Y is mid point of smaller side, so CY=1and ZB=1.
Area of 🔺 ADX =1/2(3
Explained simply:
Axyz = ab bc - ab bc/4 - ab bc/4 - ab bc/8
Axyz = ab bc - (2 ab bc/8 + 2 ab bc/8 - ab bc/8)
Axyz = 3ab*bc/8
Axyz/Aabcd = 3/8
Times 8.... --> 32x 2)=2 Sq.units Similarly Area of 🔺 XCY = 1. Sq unit And area of 🔺 ABZ =2 Sq units
Area of square - area of these 3 triangles give area of 🔺 AXZ . i .e = 8-2-2-1=3 Sq units .
As per given relation, AREA AXY= S (AREA ABCD) 3= S X 8 S= 3/8
So 8s=3
OR
Axyz = ab x bc - ab x bc/4 - ab x bc/4 - ab x bc/8
Axyz = ab x bc - (2 x ab x bc/8 + 2 x ab x bc/8 - ab x bc/8)
Axyz = 3ab x bc/8
Axyz/Aabcd = 3/8
Times 8.... --> 3
Assuming
A
B
C
D
is a parallelogram, the value of
S
can be proven as follows.
Join
B
and
D
to form segment
B
D
which is parallel to
X
Y
. The triangles
Δ
X
Y
C
and
Δ
D
B
C
are therefore similar, and since the side lengths of
Δ
X
Y
C
are half those of
Δ
D
B
C
, its area must be
4
1
of
Δ
D
B
C
, or
8
1
of
A
B
C
D
.
Join A and C now to form segment A C . Since B Y is half the length of B C , the area of Δ A B Y is half that of Δ A B C , or 4 1 of A B C D . Similarly, the area of Δ A B X is 4 1 of A B C D . Therefore, the answer is
S = 1 − 4 1 − 4 1 − 8 1 = 8 3 8 S = 3
It's also easy if you assume S is a constant for all parallelograms; you can then just assume A B C D is a square of side length 2 , and find the area of Δ A X Y is 4 − 1 − 1 − 2 1 = 2 3 . Therefore S = 4 ( 2 3 ) = 8 3