Numerical Integration Exercise - Common Region Volume Computation
A right circular cone has a base radius of and a height of . Its circular base is centered at the origin of the coordinate frame, and its axis extends upward along the -axis to its apex at . In addition, there is a sphere of radius , centered at . Find the volume of the region that is common to both the cone and the sphere. Numerical integration may be the only way to tackle this problem. Round your answer to the nearest integer.
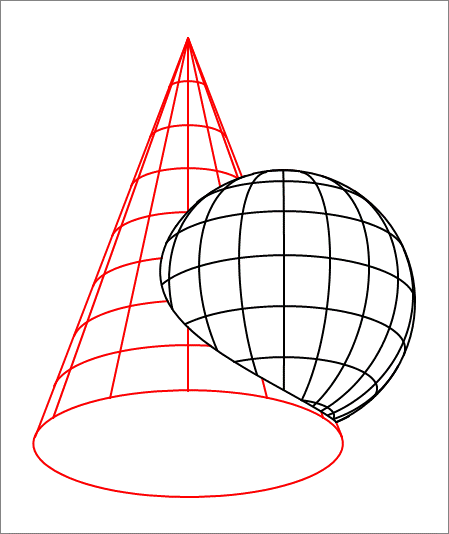
The answer is 347.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
I triple-integrated over the cone interior, using cylindrical coordinates ( r , θ , z ) . An infinitesimal volume from the cone is added to a running total if that volume also resides within the sphere. I ran trials with the cone divided into 1 0 6 pieces in the lowest-resolution case, and 1 0 9 pieces in the highest-resolution case. The common volume calculation converges to somewhere around 3 4 7 or 3 4 8 . Results are printed at the end of the code.
I also considered solving this again using Monte Carlo integration to double check, but I was too lazy.