Lateral surface area of an oblique elliptical cone
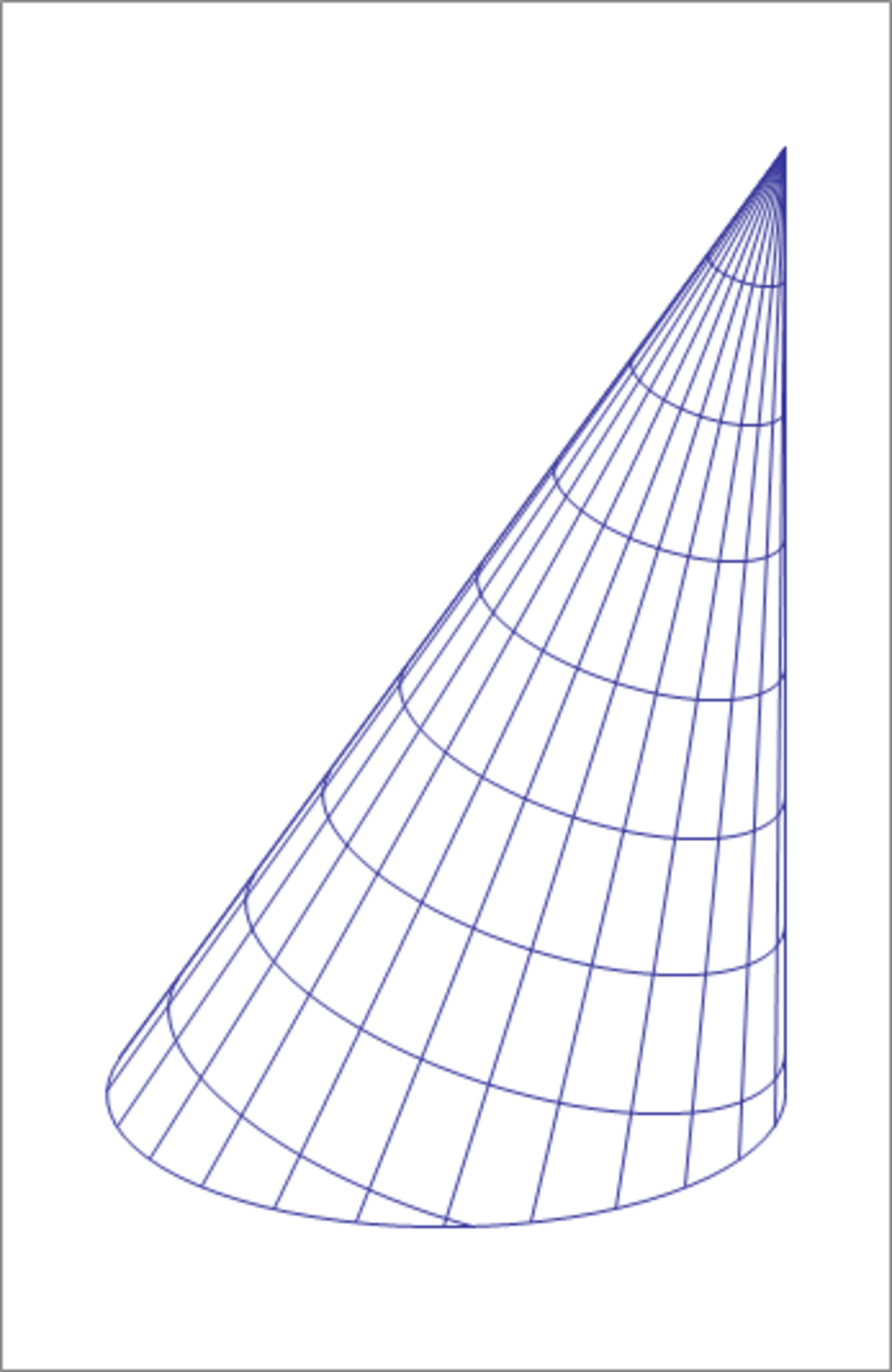
An oblique elliptical cone has its apex at and its base is a circular disc that lies in the plane, with center at , and a radius of . Find the lateral surface area of the cone.
Note: Numerical integration may be the only way to tackle this problem.
The answer is 162.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the apex be at point A . And the base is represented parametrically as b ( t ) = v 0 + v 1 cos t + v 2 sin t . In this problem A = ( 0 , 0 , 1 2 ) , v 0 = ( − 4 , 0 , 0 ) , v 1 = ( 4 , 0 , 0 ) , v 2 = ( 0 , 4 , 0 ) .
Then points on the lateral surface of the cone, are given by
p ( t , s ) = A + s ( b ( t ) − A ) = A + s ( v 0 − A + v 1 cos t + v 2 sin t ) where t ∈ [ 0 , 2 π ) and s ∈ [ 0 , 1 ] .
The surface area integral for such a parametrically defined surface is given by,
S = ∬ t , s ∣ p s × p t ∣ d t d s
where p s = ∂ s ∂ p , and p t = ∂ t ∂ p . Hence, we have,
p s = v 0 − A + v 1 cos t + v 2 sin t and p t = s ( − v 1 sin t + v 2 cos t ) . Their cross product is,
p s × p t = s ( − ( ( v 0 − A ) × v 1 ) sin t + ( ( v 0 − A ) × v 2 ) cos t + v 1 × v 2 )
Integrating with respect to s introduces a factor of 2 1 , and the integral reduces to the one-dimensional integral,
S = 2 1 ∫ 0 2 π ∣ − ( ( v 0 − A ) × v 1 ) sin t + ( ( v 0 − A ) × v 2 ) cos t + v 1 × v 2 ∣ d t
This integral can be evaluated numerically, and the final answer is S ≈ 1 6 2 . 5