Numerical Integration of Exponential Tetration
An exponential tetration is where is exponentiated by itself times.
For example,
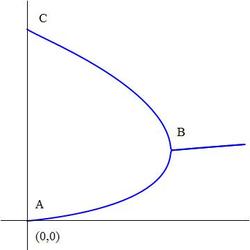
As approaches , then for some , the function bifurcates at point , splitting into the upper branch where is even and the lower branch where is odd, even though in both cases, approaches . Point is the origin and point is Let be the area of as defined by the upper and lower branches, and the line What is the floor value
Note: Use of a computer and software is expected for numerical integration. The figure above is not drawn to scale.
The answer is 454.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
This problem is a little easier to solve if we looked at the function(s) in the other way. The curve as defined by the upper and lower branches, joining at point B , can alternatively be described by the implicit equation
x x y − y = 0
where x ( y ) arches smoothly from ( 0 , 0 ) to ( 1 , 0 ) . Then any one of several possible numerical integration methods can be used, once we have an exact implicit equation. For example, given a valuie 0 ≤ y ≤ 1 , numerically determine x using the secant method, and use it as a data point for numerical integration.
The critical point B is
( e e 1 , e 1 )
as shown in the given graphic
A more straightforward way to numerically integrate this is to use a loop to exponentially tetrate 0 ≤ x ≤ e − e for some very large 2 n and 2 n + 1 , and use the difference as a data point for numerical integration. Thus, one can check the numerical results from both methods for confidence in final accuracy.
Note: The other critical point for the infinite exponential tetration is
( e e 1 , e )
which is the limit of convergence, i.e., for x > e e 1 it does not converge